天津市河北区2022-2023学年高三上学期数学期中考试试卷

试卷更新日期：2022-12-05 类型：期中考试

进入出卷网下载

一、单选题

1. 设全集 $U = {0 ， 1 ， 2 ， 3}$ ，集合 $A = {0 ， 1 ， 3}$ ， $B = {1 ， 2}$ ，则集合 $A \cap (∁_{U} B) =$ （）

A、 ${0}$ B、 ${1}$ C、 ${0 ， 3}$ D、 ${0 ， 1 ， 3}$

查看试题解析
2. 设 $x \in R$ ，则“ $x < 2$ ”是“ $x^{2} < 4$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 已知圆柱和圆锥的底面重合，且母线长相等，设圆柱、圆锥的表面积分别为S₁ ， S₂ ，则 $\frac{S_{1}}{S_{2}}$ 的值为（）

A、 $\frac{1}{2}$ B、1 C、2 D、3

查看试题解析
4. 某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300]分组得到如下频率分布直方图，则直方图中x的值为（）

A、0.007 B、0.0075 C、0.008 D、0.0085

查看试题解析
5. 函数 $f (x) = \frac{\ln | x |}{e^{x} - e^{- x}}$ 的部分图像大致为（）

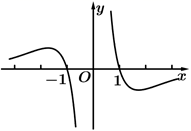A、 B、 C、 D、

查看试题解析
6. 若 $a = \ln 2$ ， $b = 3^{0.2}$ ， $c = \log_{0.3} 2$ ，则a ， b ， c的大小关系为（）

A、 $a < b < c$ B、 $b < a < c$ C、 $c < a < b$ D、 $c < b < a$

查看试题解析
7. 若双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的一条渐近线方程为 $y = \frac{\sqrt{5}}{2} x$ ，则双曲线C的离心率为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{3}{2}$ D、2

查看试题解析
8. 若实数a ， b满足 $\lg a + \lg b = \lg (a + 2 b)$ ，则ab的最小值为（）

A、8 B、6 C、4 D、2

查看试题解析
9. 已知函数 $f (x) = \frac{| x |}{x^{2} + 1}$ ，给出下面四个结论：
① $f (x)$ 的定义域是 $(- \infty ， + \infty)$ ；

② $f (x)$ 是偶函数；

③ $f (x)$ 在区间 $(0 ， + \infty)$ 上单调递增；

④ $f (x)$ 的图像与 $g (x) = \frac{1}{4}$ 的图像有4个不同的交点.

其中正确的结论是（）

A、①② B、③④ C、①②③ D、①②④

查看试题解析

二、填空题

10. i是虚数单位，则复数 $\frac{1 - i}{1 - 2 i} =$ .

查看试题解析
11. ${(\frac{1}{x} - \sqrt{x})}^{8}$ 的展开式中含x项的系数为.

查看试题解析
12. 求经过点M(2， $2 \sqrt{3}$ )且与圆x²＋y²=4相切的直线的方程为．

查看试题解析
13. 一盒子装有4件产品，其中有3件一等品，1件二等品.从中不放回地抽取两次，每次任取一件，设事件A为“第一次取到的是一等品”，事件B为“第二次取到的是一等品”，则条件概率 $P (B | A)$ 的值为.

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} 2^{x - 3} + 1 ， x \leq 3 \\ \log_{2} (x + 1) ， x > 3 \end{array}$ 满足 $f (a) = 3$ ，则 $f (a - 5)$ 的值为.

查看试题解析
15. 如图，在四边形ABCD中， $A D = 4$ ， $A B = 2$ ，若 $△ A B C$ 是等边三角形，且 $A D ∥ B C$ ， E是CD的中点，则 $\vec{A E} \cdot \vec{B D}$ 的值为.

查看试题解析

三、解答题

16. 已知函数 $f (x) = \sqrt{3} \sin (2 x + \frac{π}{3}) - \cos 2 x$ ， $x \in R$ .

(1)、求函数 $f (x)$ 的最小正周期；

(2)、求函数 $f (x)$ 的单调递减区间.

查看试题解析
17. 已知 $a ， b ， c$ 分别是 $△ A B C$ 的内角 $A ， B ， C$ 的对边，且 $\frac{a}{b} = \frac{\cos A}{2 - \cos B}$ ．

(1)、求 $\frac{a}{c}$ ．

(2)、若 $b = 4$ ， $\cos C = \frac{1}{4}$ ，求 $△ A B C$ 的面积．

(3)、在（2）的条件下，求 $\cos (2 C + \frac{π}{3})$ 的值．

查看试题解析
18. 如图，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的底面为直角三角形， $A A_{1} = 2 A B = 2 B C = 2$ ， E ， F分别为AB ， $C C_{1}$ 的中点.

(1)、求证： $E F //$ 平面 $A B_{1} C_{1}$ ；

(2)、求直线BF与平面 $A B_{1} C_{1}$ 所成角的正弦值；

(3)、求平面 $A B_{1} C_{1}$ 与平面 $B_{1} C_{1} C B$ 夹角的余弦值.

查看试题解析
19. 已知数列 ${a_{n}}$ 为等差数列，且 $a_{2} = 3$ ， $a_{4} + a_{5} + a_{6} = 0$

(1)、求数列 ${a_{n}}$ 的通项 $a_{n}$ ，及前 $n$ 项和 $S_{n}$

(2)、请你在数列 ${a_{n}}$ 的前4项中选出三项，组成公比的绝对值小于1的等比数列 ${b_{n}}$ 的前3项，并记数列 ${b_{n}}$ 的前n项和为 ${T_{n}}$ ．若对任意正整数 $k ， m ， n$ ，不等式 $S_{m} < T_{n} + k$ 恒成立，试求 $k$ 的最小值．

查看试题解析