2022-2023学年浙教版数学七年级上册6.7角的和差课后测验

试卷更新日期：2022-12-04 类型：同步测试

进入出卷网下载

一、单选题

1. 关于角的描述不正确的是（）

A、∠1与∠AOB表示同一个角 B、∠AOC可以用∠O表示 C、∠AOC＝∠AOB+∠BOC D、∠β表示∠BOC

查看试题解析
2. 如图，将一副三角板的直角顶点重合，摆放在桌面上， ∠AOD = 130°，则∠BOC =（）

A、20° B、30° C、40° D、50°

查看试题解析
3. 将一副三角板按如图方式摆放在一起，若∠2=30°15ˊ，则∠1的度数等于（）

A、59.45° B、60°15ˊ C、59°45ˊ D、59.75°

查看试题解析
4. 把一副三角板按如图所示方式拼在一起，并作 $∠ A B E$ 的平分线 $B M$ ，则 $∠ C B M$ 的度数是（）

A、120° B、60° C、30° D、15°

查看试题解析
5. 用一副三角板画角，不能画出的角是（）

A、15° B、75° C、145° D、165°

查看试题解析
6. 如图，长方形纸片ABCD，点E、F分别在边AB、CD上，连接EF．将∠BEF对折，点B落在直线EF上的点B' 处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A' 处，得折痕EN．则∠NEM的度数为（）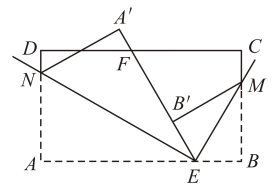

A、105^o B、 $90 °$ C、 $60 °$ D、不能确定

查看试题解析
7. 如图， $O A ⊥ O C ， O B ⊥ O D$ ，4位同学观察图形后各自观点如下．甲： $∠ A O B = ∠ C O D$ ；乙： $∠ B O C + ∠ A O D = 180 °$ ；丙： $∠ A O B + ∠ C O D = 90 °$ ；丁：图中小于平角的角有6个；其中正确的结论是（）

A、甲、乙、丙 B、甲、乙、丁 C、乙、丙、丁 D、甲、丙、丁

查看试题解析
8. 将一张长方形纸片ABCD按如图所示的方式折叠，AE、AF为折痕，点B、D折叠后的对应点分别为 $B ′$ 、 $D ′$ ，若 $∠ B^{'} A D^{'}$ ＝10°，则∠EAF的度数为（）

A、40° B、45° C、50° D、55°

查看试题解析
9. 如图，点 $O$ 为线段 $A D$ 外一点，点 $M$ ， $C$ ， $B$ ， $N$ 为 $A D$ 上任意四点，连接 $O M$ ， $O C$ ， $O B$ ， $O N$ ，下列结论错误的是（）

A、以 $O$ 为顶点的角共有15个 B、若 $M C = C B$ ， $M N = N D$ ，则 $C D = 2 C N$ C、若 $M$ 为 $A B$ 中点， $N$ 为 $C D$ 中点，则 $M N = \frac{1}{2} (A D - C B)$ D、若 $O M$ 平分 $∠ A O C$ ， $O N$ 平分 $∠ B O D$ ， $∠ A O D = 5 ∠ C O B$ ，则 $∠ M O N = \frac{3}{2} (∠ M O C + ∠ B O N)$

查看试题解析
10. 如图，∠AOB=α ， OA₁、OB₁分别是∠AOM和∠MOB的平分线，OA₂、OB₂分别是∠A₁OM和∠MOB₁的平分线，OA₃、OB₃分别是∠A₂OM和∠MOB₂的平分线，…，OA_n、分别是∠A_n_-1OM和∠MOB_n_-1的平分线，则∠A_nOB_n的度数是（）

A、 $\frac{a}{n}$ B、 $\frac{a}{2^{n - 1}}$ C、 $\frac{a}{2^{n}}$ D、 $\frac{a}{n^{2}}$

查看试题解析

二、填空题

11. 如图， $∠ A O B$ 的度数是 $°$ .

查看试题解析
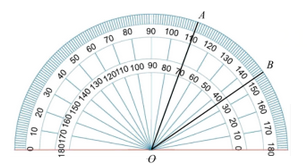12. 如图，OC平分∠AOB，若∠BOC＝29°，则∠AOB＝°.

查看试题解析
13. 如图，射线OC平分∠AOB， $∠ A O B = 40 ° 3 6^{'}$ ，则∠AOC的度数为．

查看试题解析
14. 如图，OD平分∠AOB，OE平分∠BOC，若∠COD=100°，∠AOE=110°，则∠DOE= ．

查看试题解析
15. 北京西站和北京南站是北京的两个铁路客运中心，如图，A，B，C分别表示天安门、北京西站、北京南站，经测量，北京西站在天安门的南偏西77°方向，北京南站在天安门的南偏西18°方向.则∠BAC=°.

查看试题解析
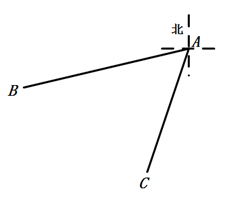16. 将一张长方形的纸按照如图所示折叠后，点C、D两点分别落在点C'、D'处，若EA平分∠D'EF，则∠DEF= 。

查看试题解析
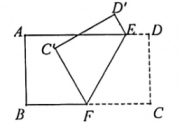17. 如图，A、B、C为直线l上的点，D为直线l外一点，若 $∠ A B D ＝ 2 ∠ C B D$ ，则 $∠ C B D$ 的度数为．

查看试题解析
18. 如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD=150°，则∠BOC等于度．

查看试题解析
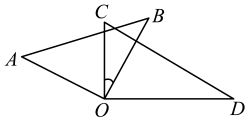19. 如图，将一副三角板摆放在直线AB上， $∠ E C D = ∠ F D G = 90 °$ ， $∠ E D C = 45 °$ ，设 $∠ E D F = x$ ，则用x的代数式表示 $∠ G D B$ 的度数为.

查看试题解析
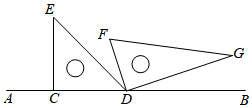20. 如图，点C，D在线段BE上（C在D的左侧），点A在线段BE外，连接AB，AC，AD，AE，已知∠BAE ＝ 120°，∠CAD ＝ 60°，有下列说法：①直线CD上以B，C，D，E为端点的线段共有6条；②作∠BAM＝ $\frac{1}{2}$ ∠BAD，∠EAN＝ $\frac{1}{2}$ ∠EAC.则∠MAN＝30°；③以A为顶点的所有小于平角的角的度数和为420°；④若BC＝2，CD＝DE＝3，点F是线段BE上任意一点，则点F到点B，C，D，E的距离之和最大值为17，最小值为11.其中说法正确的有 .（填上所有正确说法的序号）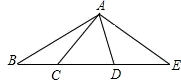

查看试题解析

三、计算题

21. 计算： $33 ° 16' 28'' + 24 ° 46' 37''$ .

查看试题解析
22. 计算 $56 ° 1 7^{'} + 12 ° 4 5^{'} - 16 ° 2 1^{'}$ ．

查看试题解析

四、解答题

23. 如图，∠AOB是平角， $∠ A O C = 80 °$ ， $∠ B O D = 30 °$ ，OM、ON外别是∠AOC、∠BOD的平分线，求∠MON的度数.

查看试题解析
24. 如图，在△ABC中，AD是角平分线，AE是BC边上的高，∠B=40°，∠C=68°．求∠DAE的度数．

查看试题解析
25. 如图，已知 $O C$ 是 $∠ A O B$ 内部的一条射线， $O D$ 是 $∠ A O B$ 的角平分线， $∠ A O C$ 与 $∠ B O C$ 的度数比为 $3$ ∶ $2$ ，且 $∠ D O C = 12 °$ ，求 $∠ A O B$ 的度数．（请同学们利用两种不同的方法解答此题，其中一种方法用方程求解）

查看试题解析
26. 如图1， $△ A B C$ 中， $∠ A C B = 90 °$ ，点D在 $A B$ 上，且 $∠ B A C = 2 ∠ D C B$ ，求证： $A C = A D$ ．小明发现，除了直接用角度计算的方法外，还可以用下面两种方法：
方法1：如图2，作 $A E$ 平分 $∠ C A B$ ，与 $C D$ 相交于点E．

方法2：如图3，作 $∠ D C F = ∠ D C B$ ，与 $A B$ 相交于点F．

(1)、根据阅读材料，分别运用以上两种方法，证明 $A C = A D$ ．

(2)、用学过的知识或参考小明的方法，解决下面的问题：
如图4， $△ A B C$ 中，点D在 $A B$ 上，点E在 $B C$ 上，且 $∠ B D E = 2 ∠ A B C$ ，点F在 $B D$ 上，且 $∠ A F E = ∠ B A C$ ，延长 $D C 、 F E$ ，相交于点G，且 $∠ D G F = ∠ B D E$ ．在图中找出与 $∠ D E F$ 相等的角，并加以证明．

查看试题解析

2022-2023学年浙教版数学七年级上册6.7角的和差 课后测验

一、单选题

二、填空题

三、计算题

四、解答题

2022-2023学年浙教版数学七年级上册6.7角的和差课后测验