江苏省南京市江宁区五校2022-2023学年高三上学期数学期中联考试卷
试卷更新日期:2022-12-02 类型:期中考试
一、单选题
-
1. 若集合 , 则( )A、 B、 C、 D、2. 设复数满足 , 则( )A、 B、 C、 D、3. 在 的展开式中,常数项为( )A、15 B、 C、30 D、4. 我国古代建筑的屋顶对建筑立面起着特别重要的作用,古代建筑屋顶主要有庑殿式、硬山顶、歇山顶、悬山顶攒尖顶、盝顶、卷棚顶等类型,其中硬山式屋顶造型的最大特点是比较简单、朴素,只有前后两面坡,而且屋顶在山墙墙头处与山墙齐平,没有伸出部分,山面裸露没有变化.硬山式屋顶(如图1)可近似地看作直三棱柱(如图2),其高为 , 到平面的距离为 , 为 , 则可估算硬山式屋顶的体积约为( )
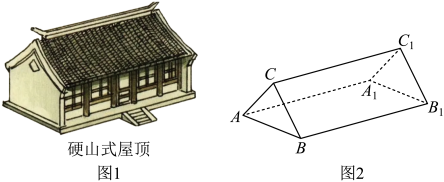 A、 B、 C、 D、5. 函数的图象大致为( )A、
A、 B、 C、 D、5. 函数的图象大致为( )A、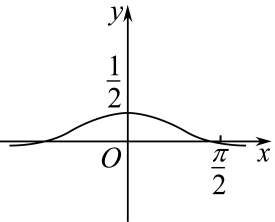 B、
B、 C、
C、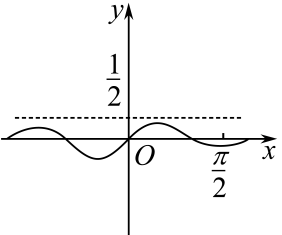 D、
D、 6. 若 , 则( )A、 B、 C、 D、7. 已知菱形的边长为2, , 是菱形内一点, 若 , 则( )A、 B、 C、 D、28. 设 , , , 则( )A、 B、 C、 D、
6. 若 , 则( )A、 B、 C、 D、7. 已知菱形的边长为2, , 是菱形内一点, 若 , 则( )A、 B、 C、 D、28. 设 , , , 则( )A、 B、 C、 D、二、多选题
-
9. 下列命题为真命题的是( )A、 B、“”是“”的充分条件 C、若 , 则 D、若 , 则10. 已知等比数列的公比为 , 前项积为 , 若 , 且 , 则下列命题正确的是( )A、 B、当且仅当时,取得最大值 C、 D、11. 已知函数的最小正周期为 , 且对于恒成立,则( )A、在区间单调递减 B、在区间有两个零点 C、是曲线的一个对称中心 D、当时,函数取得极值12. 已知函数满足:对于任意实数 , 都有 , 且 , 则( )A、是奇函数 B、是偶函数 C、是曲线的一个对称中心 D、
三、填空题
-
13. 设函数则 .14. 在正方体中,为棱的中点,则与平面所成角的正弦值为 .15. 若斜率为的直线与轴交于点 , 与圆相交于点两点,若 , 则 .16. 设圆锥的底面半径为2,母线长为 , 若正四棱柱上底面的4个顶点在其母线上,下底面的4个顶点在其底面圆内,则该正四棱柱体积的最大值为 .
四、解答题
-
17. 在中,角A,B,C所对的边分别为a,b,c.已知 , .(1)、求的值;(2)、D为边的中点,若 , 求的面积.18. 已知等差数列的前项和为 , 且 , .(1)、求数列的通项公式;(2)、设 , 求数列的前项和 .19. 随着人们对环境关注度的提高,绿色低碳出行越来越受市民重视,为此某市建立了共享电动车服务系统,共享电动车是一种新的交通工具,这是新时代下共享经济的促成成果.目前来看,共享电动车的收费方式通过客户端软件和在线支付工具完成付费流程,从开锁到还车所用的时间称为一次租用时间,具体计费标准如下:
①租用时间30分钟2元,不足30分钟按2元计算;
②租用时间为30分钟以上且不超过40分钟,按4元计算;
③租用时间为40分钟以上且不超过50分钟,按6元计算
甲、乙两人独立出行,各租用公共电动车一次,租用时间都不会超过50分钟,两人租用时间的概率如下表:
租用时间
不超过30分钟
甲
乙
若甲、乙租用时间相同的概率为 .
(1)、求 , 的值;(2)、设甲、乙两人所付费之和为随机变量 , 求的分布列和数学期望.
