浙江省金华五中2022-2023学年九年级上学期数学期中试卷
试卷更新日期:2022-12-02 类型:期中考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. -2022的绝对值是( ).A、 B、-2022 C、2022 D、2. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 科克曲线
B、
科克曲线
B、 笛卡尔心形线
C、
笛卡尔心形线
C、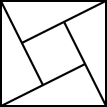 赵爽弦图
D、
赵爽弦图
D、 斐波那契螺旋线
3. 如图,过直线外一点作已知直线的平行线,其依据是( )
斐波那契螺旋线
3. 如图,过直线外一点作已知直线的平行线,其依据是( ) A、同旁内角互补,两直线平行 B、内错角相等,两直线平行 C、两点确定一条直线 D、同位角相等,两直线平行4. 一个不透明的袋中有4个白球,3个黄球和2个红球,这些球除颜色外其余都相同,则从袋中随机摸出一个球是黄球的概率为( )A、 B、 C、 D、5. 分式的值为0,则 x=( )A、3 B、-3 C、2 D、-26. “儿童放学归来早,忙趁东风放纸鸢”,小明周末在婺州公园草坪上放风筝,已知风筝拉线长100米且拉线与地面夹角为65°(如图所示,假设拉线是直的,小明身高忽略不计),则风筝离地面的高度可以表示为 ( )
A、同旁内角互补,两直线平行 B、内错角相等,两直线平行 C、两点确定一条直线 D、同位角相等,两直线平行4. 一个不透明的袋中有4个白球,3个黄球和2个红球,这些球除颜色外其余都相同,则从袋中随机摸出一个球是黄球的概率为( )A、 B、 C、 D、5. 分式的值为0,则 x=( )A、3 B、-3 C、2 D、-26. “儿童放学归来早,忙趁东风放纸鸢”,小明周末在婺州公园草坪上放风筝,已知风筝拉线长100米且拉线与地面夹角为65°(如图所示,假设拉线是直的,小明身高忽略不计),则风筝离地面的高度可以表示为 ( ) A、 B、 C、 D、7. 如图,点、、在上, , , 则的度数是 ( )
A、 B、 C、 D、7. 如图,点、、在上, , , 则的度数是 ( )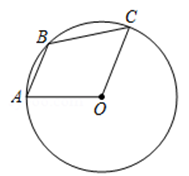 A、 B、 C、 D、8. 已知抛物线对称轴是直线 , 与轴两个交点间的距离为2,将此抛物线先向左平移2个单位,再向下平移3个单位,则所得新抛物线与轴两个交点间的距离为( )A、2 B、3 C、4 D、59. 如图,矩形纸片中, , 是上一点,连结 , 沿直线翻折后点落到点 , 过点作 , 垂足为 . 若 , 则的值为( )
A、 B、 C、 D、8. 已知抛物线对称轴是直线 , 与轴两个交点间的距离为2,将此抛物线先向左平移2个单位,再向下平移3个单位,则所得新抛物线与轴两个交点间的距离为( )A、2 B、3 C、4 D、59. 如图,矩形纸片中, , 是上一点,连结 , 沿直线翻折后点落到点 , 过点作 , 垂足为 . 若 , 则的值为( )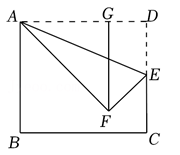 A、 B、 C、5 D、10. 如图,等腰中, , 点是外一点,分别以 , 为斜边作两个等腰直角和 , 并使点落在上,点落在的内部,连结 . 若 , 则与的面积之比为 ( )
A、 B、 C、5 D、10. 如图,等腰中, , 点是外一点,分别以 , 为斜边作两个等腰直角和 , 并使点落在上,点落在的内部,连结 . 若 , 则与的面积之比为 ( )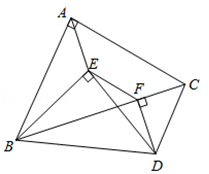 A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题 (本题有6小题,每小题4分,共24分)
-
11. 因式分解: .12. 已知 , 则 .13. 已知扇形的圆心角为 , 弧长为 , 则它的面积为 .14. 如图,在直角坐标系 中,正方形 的边 在 轴上,点 , .现固定点 在 轴上的位置不变,把正方形沿箭头方向推,使点 落在 轴正半轴上的点 ,则点 的对应点 的坐标为.
 15. 如图,点A在反比例函数 (k>0, x>0)的图象上,AB⊥y轴于点B,C为x轴正半轴上一点,将△ABC绕点A旋转180°得到△AED,点C的对应点D恰好落在函数图象上.若△BOC的面积为6,则k的值为.
15. 如图,点A在反比例函数 (k>0, x>0)的图象上,AB⊥y轴于点B,C为x轴正半轴上一点,将△ABC绕点A旋转180°得到△AED,点C的对应点D恰好落在函数图象上.若△BOC的面积为6,则k的值为. 16. 飞机导航系统的正常工作离不开人造卫星的信号传输(如图1).五颗同轨道同步卫星,其位置 , , , , , 如图2所示.是它们的运行轨道,弧度数为 , 点到点和点的距离相等,于 , 交于 , 交于 , 连结 , , 已知一架飞机从飞到的直线距离为4千公里,则轨道的半径为千公里,当时,则线段 , 的长度之和为 千公里.
16. 飞机导航系统的正常工作离不开人造卫星的信号传输(如图1).五颗同轨道同步卫星,其位置 , , , , , 如图2所示.是它们的运行轨道,弧度数为 , 点到点和点的距离相等,于 , 交于 , 交于 , 连结 , , 已知一架飞机从飞到的直线距离为4千公里,则轨道的半径为千公里,当时,则线段 , 的长度之和为 千公里.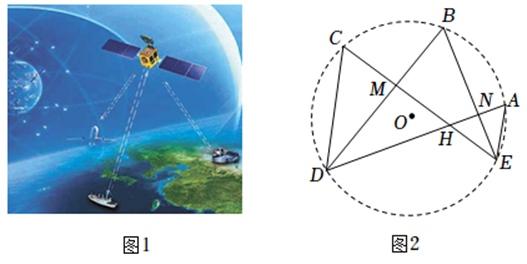
三、解答题 (本题有8小题,共66分)
-
17. 计算:18. 解不等式组 .19. 如图,在平行四边形中,对角线AC,BD交于点O,AB=6,AD=10,AC=8.
 (1)、求∠BAC的度数;(2)、设求的值.20. 为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(未完成),解答下列问题:
(1)、求∠BAC的度数;(2)、设求的值.20. 为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(未完成),解答下列问题: (1)、若组的频数比组小24,则 , ;(2)、扇形统计图中,部分所对的圆心角为 , 求的值并补全频数分布直方图;(3)、若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?21. 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)、若组的频数比组小24,则 , ;(2)、扇形统计图中,部分所对的圆心角为 , 求的值并补全频数分布直方图;(3)、若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?21. 如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.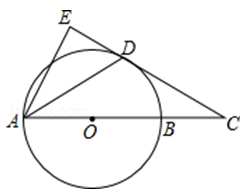 (1)、求证:直线CE是⊙O的切线.(2)、若BC=3,CD=3 , 求半径OB与线段AE的长.22. 某游泳馆有以下两种购票方式:一是普通门票每张30元;二是置办年卡(从购买日起,可持年卡使用一年).年卡每张m元(480≤m≤550,m为整数),且年卡持有者每次进入时,还需购买一张固定金额的入场券.设市民在一年中去游泳馆x次,购买普通门票和年卡所需的总费用分别为y1(元)和y2(元).
(1)、求证:直线CE是⊙O的切线.(2)、若BC=3,CD=3 , 求半径OB与线段AE的长.22. 某游泳馆有以下两种购票方式:一是普通门票每张30元;二是置办年卡(从购买日起,可持年卡使用一年).年卡每张m元(480≤m≤550,m为整数),且年卡持有者每次进入时,还需购买一张固定金额的入场券.设市民在一年中去游泳馆x次,购买普通门票和年卡所需的总费用分别为y1(元)和y2(元).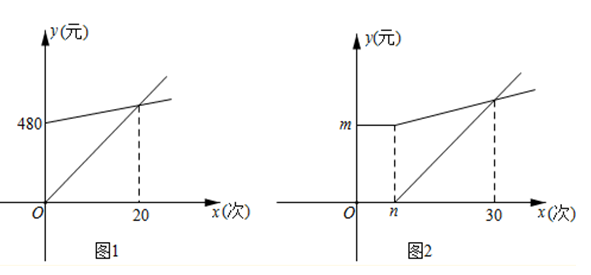 (1)、如图1,若m=480,当x=20时,两种购票方式的总费用y1与y2相等.
(1)、如图1,若m=480,当x=20时,两种购票方式的总费用y1与y2相等.①分别求y1 , y2关于x的函数表达式.
②要使市民办年卡比购买普通门票的总费用至少节省144元,则该市民当年至少要去游泳馆多少次?
(2)、为增加人气,该游泳馆推出了每位顾客n(n<30)次免费体验活动,如图2.某市民发现在这一年进游泳馆的次数达到30次(含免费体验次数)时,两种购票方式的总费用y1与y2相等,求所有满足条件的m的值.23. 如图,已知抛物线经过 , 两点,直线交轴于点 , 交抛物线于点 . (1)、求该抛物线的解析式;(2)、点在抛物线上,点在直线上,若以 , , , 为顶点的四边形是平行四边形,求点的坐标;(3)、若 , , 三点到同一条直线的距离分别是 , , , 问是否存在直线 , 使?若存在,请直接写出的值;若不存在,请说明理由.24. 如图,两个正方形ABCD与EFGH,AD与EF的中点都是O.
(1)、求该抛物线的解析式;(2)、点在抛物线上,点在直线上,若以 , , , 为顶点的四边形是平行四边形,求点的坐标;(3)、若 , , 三点到同一条直线的距离分别是 , , , 问是否存在直线 , 使?若存在,请直接写出的值;若不存在,请说明理由.24. 如图,两个正方形ABCD与EFGH,AD与EF的中点都是O. (1)、如图1,点D与G重合.
(1)、如图1,点D与G重合.①求的值.
②连结BH,求tan∠ABH的值.
(2)、如图2,若AB=EF=6,在正方形EFGH绕点O旋转过程中,以E,C,H为顶点的三角形能否是等腰三角形?若能,求出该三角形面积;若不能,说明理由.