浙江省舟山市普陀二中2022-2023学年九年级上学期11月月考数学试题卷
试卷更新日期:2022-12-02 类型:月考试卷
一、选择题(本大题共10小题,每小题3分.)
-
1. 若 , 则的值为( )A、 B、 C、 D、2. 下列事件是必然事件的是( )A、下个月1号会下雨 B、13个人中至少有2人生日在同一个月 C、平分弦的直径垂直于弦 D、从一副扑克牌中随机抽取一张,抽到红桃3. 下列关系式中,属于二次函数的是( )A、 B、 C、 D、4. 下列说法中,正确的是( )A、长度相等的弧是等弧 B、圆的每一条直径都是它的对称轴 C、直径如果平分弦就一定垂直弦 D、直径所对的弧是半圆5. 把二次函数的图象向右平移2个单位后,再向上平移3个单位所得图象的函数表达式是( )A、 B、 C、 D、6. 下列命题正确的个数有( )
①两边成比例且有一角对应相等的两个三角形相似;②对角线相等的四边形是矩形;③任意四边形的中点四边形是平行四边形;④两个相似多边形的面积比为2:3,则周长比为4:9.
A、1个 B、2个 C、3个 D、4个7. 阅读理解:如图1,在平面内选一定点O,引一条有方向的射线 , 再选定一个单位长度,那么平面上任一点M的位置可由的度数与的长度m确定,有序数对称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线上,则正六边形的顶点C的极坐标应记为( )
 A、 B、 C、 D、8. 如图,在矩形ABCD中,已知 , , 矩形在直线l上绕其右下角的顶点B向右旋转至图①位置,再绕右下角的顶点继续向右旋转至图②位置,…,以此类推,这样连续旋转2021次后,顶点A在整个旋转过程中所经过的路程之和是( )
A、 B、 C、 D、8. 如图,在矩形ABCD中,已知 , , 矩形在直线l上绕其右下角的顶点B向右旋转至图①位置,再绕右下角的顶点继续向右旋转至图②位置,…,以此类推,这样连续旋转2021次后,顶点A在整个旋转过程中所经过的路程之和是( )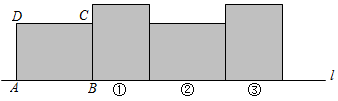 A、 B、 C、 D、9. 二次函数的图象如图所示,对称轴是直线 , 则下列结论:①;②;③;④;⑤(m为实数).正确的有( )个
A、 B、 C、 D、9. 二次函数的图象如图所示,对称轴是直线 , 则下列结论:①;②;③;④;⑤(m为实数).正确的有( )个 A、1 B、2 C、3 D、410. 已知关于x的一元二次方程有一个根是1,若的顶点在第一象限,设 , 则t的取值范围是( )A、 B、 C、 D、
A、1 B、2 C、3 D、410. 已知关于x的一元二次方程有一个根是1,若的顶点在第一象限,设 , 则t的取值范围是( )A、 B、 C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
11. 舟山市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数n
30
75
130
210
480
856
1250
2300
发芽数m
28
72
125
200
457
814
1187
2185
发芽频率
0.9333
0.9600
0.9615
0.9524
0.9521
0.9509
0.9496
0.9500
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是(结果精确到0.01).
12. 大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”黄金比为 , 如图,为的黄金分割点(),如果的长度为 , 那么较长线段的长度为(结果精确到). 13. 如图,在扇形中,点C、D在上,连接、交于点E,若 , 的度数为 , 则°.
13. 如图,在扇形中,点C、D在上,连接、交于点E,若 , 的度数为 , 则°. 14. 如图, 是半圆O的直径,C、D是半圆上两点,且满足 , ,则 .
14. 如图, 是半圆O的直径,C、D是半圆上两点,且满足 , ,则 . 15. 如图,平行于x轴的直线分别交抛物线与于B,C两点,过点C作y轴的平行线交于点D,直线交于点E,则的值是 .
15. 如图,平行于x轴的直线分别交抛物线与于B,C两点,过点C作y轴的平行线交于点D,直线交于点E,则的值是 . 16. 如图,已知点 , , , 在函数位于第二象限的图象上,点 , , , 在函数位于第一象限的图象上,点 , , , 在轴的正半轴上,若四边形、 , , 都是正方形,则正方形的对角线长为 .
16. 如图,已知点 , , , 在函数位于第二象限的图象上,点 , , , 在函数位于第一象限的图象上,点 , , , 在轴的正半轴上,若四边形、 , , 都是正方形,则正方形的对角线长为 .
三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)
-
17. 已知 .(1)、若 , 求 , 的值;(2)、若 , 求的值.18. 如图,已知在平面直角坐标系中,的三个顶点的坐标分别为 , , .

⑴画出关于原点成中心对称的 , 并写出点的坐标;
⑵画出将绕点按顺时针方向旋转所得的并写出点的坐标.
19. 某校以“我最喜爱的书籍”为主题,对全校学生进行随机抽样调查,每个被调查的学生必须区从“科普、绘画、诗歌、散文”四类书籍中选择最喜爱的一类.学校将调查结果绘制成如下两幅不完整的统计图:
请根据图中信息解答下列问题:
(1)、本次被调查的学生有人.(2)、扇形统计图中,“散文”类所对应的圆心角的度数为 ▲ . 请补全条形统计图.(3)、最喜爱“科普”类的4名学生中有1名女生、3名男生,现从4名学生中随机抽取2人参加学校举办的科普知识宣传活动,请用列表或画树状图的方法求出所选的2人恰好都是男生的概率.20. 如图,在中, , 以为直径的交于点D,延长交于点E.连接交于点F. (1)、求证:是等腰三角形.(2)、当 , 时,求的长.21. 某超市经销一种销售成本为每件40元的商品,据市场调查分析,如果按每件50元销售,一周能售出500件,若销售单价每涨1元,每周销量就减少10件,设销售单价为x元(),一周的销售量为y件.(1)、写出y与x的函数关系式:(标明x的取值范围);(2)、设一周的销售利润为S,写出S与x的函数关系式,并确定当单价是多少时利润最大;(3)、在超市对该种商品投入不超过12000元的情况下,使得一周销售利润为8000元,销售单价应定为多少元?22. 如图,抛物线交x轴于点和点B,交y轴于点 .
(1)、求证:是等腰三角形.(2)、当 , 时,求的长.21. 某超市经销一种销售成本为每件40元的商品,据市场调查分析,如果按每件50元销售,一周能售出500件,若销售单价每涨1元,每周销量就减少10件,设销售单价为x元(),一周的销售量为y件.(1)、写出y与x的函数关系式:(标明x的取值范围);(2)、设一周的销售利润为S,写出S与x的函数关系式,并确定当单价是多少时利润最大;(3)、在超市对该种商品投入不超过12000元的情况下,使得一周销售利润为8000元,销售单价应定为多少元?22. 如图,抛物线交x轴于点和点B,交y轴于点 . (1)、求抛物线的函数表达式;(2)、若点M在抛物线上,且 , 求点M的坐标.23. 综合与实践:动手操作:某校八(1)班数学课外兴趣小组在学完第13章的特殊三角形后,利用手头上的一副三角板,他们将一块直角三角板( , )的直角顶点放置在另一块直角三角板( , )斜边的中点处,并将三角板绕点任意旋转.
(1)、求抛物线的函数表达式;(2)、若点M在抛物线上,且 , 求点M的坐标.23. 综合与实践:动手操作:某校八(1)班数学课外兴趣小组在学完第13章的特殊三角形后,利用手头上的一副三角板,他们将一块直角三角板( , )的直角顶点放置在另一块直角三角板( , )斜边的中点处,并将三角板绕点任意旋转.发现结论:
(1)、如图,三角板的两边分别与另一块三角板的边交于点(规定:此时点均在边上运动),他们在旋转过程中,发现线段与的长总相等及四边形的面积不会发生变化.
问题解决:
①请你帮他们说明的理由;
②若 , 请你帮他们求出四边形的面积.
(2)、拓展延伸:
如图,连接 , 当 , 时,那么直角三角板在绕点旋转一周的过程中,请你直接写出线段长的最小值和最大值. 24. 如图1,点是正方形的中心,点是边上一动点,在上截取 , 连结 , .
24. 如图1,点是正方形的中心,点是边上一动点,在上截取 , 连结 , . (1)、初步探究:在点的运动过程中:
(1)、初步探究:在点的运动过程中:
猜想线段与的关系,并说明理由.(2)、深入探究:
如图2,连结 , 过点作的垂线交于点 . 交的延长线于点 . 延长交的延长线于点 .①直接写出的度数.
②若 , 请探究的值是否为定值,若是,请求出其值;反之,请说明理由