浙江省义乌市三校联考2022-2023学年七年级上学期数学期中试卷

试卷更新日期：2022-12-02 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. -2的相反数是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、-1

查看试题解析
2. 据统计我国每年浪费的粮食约35000000吨，我们要勤俭节约，反对浪费，积极的加入“光盘行动”中来.用科学记数法表示35000000是（）.

A、3.5×10⁶ B、3.5×10⁷ C、35×10⁶ D、35×10⁷

查看试题解析
3. 在实数- $\frac{2}{3}$ ， $\sqrt{5}$ ， 0，π， $\sqrt[3]{27}$ ， -3.1414， $\sqrt{8}$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 多项式 $2^{3} + 7 x + 4 y$ 的次数为多少（）

A、5次 B、3次 C、2次 D、1次

查看试题解析
5. 下列计算正确的是（）

A、 $5 a b - 2 a = 3 b$ B、 $a + a = a^{2}$ C、 $2 a b + 3 b a = 5 a b$ D、 $7 x^{2} y - 7 x y^{2} = 0$

查看试题解析
6. 若代数式 $x - 2 y + 2$ 的值是5，则代数式 $4 y - 2 x + 1$ 的值是（）

A、-4 B、-7 C、-5 D、不能确定

查看试题解析
7. 下列说法中：①立方根等于本身的是-1，0，1； ②平方根等于本身的数是0，1；③两个无理数的和一定是无理数； ④实数与数轴上的点是一一对应的；⑤ $\frac{π}{- 3}$ 是负分数；其中正确的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
8. 有一个人患了流感，经过两轮传染后有若干人被传染上流感．假设在每轮的传染中平均一个人传染了m个人，则第二轮被传染上流感的人数是（）

A、 $m + 1$ B、 ${(m + 1)}^{2}$ C、 $m (m + 1)$ D、 $m^{2}$

查看试题解析
9. 定义一种对正整数 $n$ 的“F”运算： ①当 $n$ 为奇数时， $F_{(n)} = 3 n + 1$ ； ②当 $n$ 为偶数时， $F_{(n)} = \frac{n}{2^{k}}$ (其中 $k$ 是使 $F_{(n)}$ 为奇数的正整数) ……，两种运算交替重复进行．例如：取 n=24，则：

若 $n = 22$ ，则第 2021 次“F”运算的结果是（）

A、1 B、4 C、22 D、 $2^{2020}$

查看试题解析
10. 将图1中周长为36的长方形纸片剪成1号、2号、3号、4号正方形和5号长方形，并将它们按图2的方式放入周长为55的长方形中，则没有覆盖的阴影部分的周长为（）

A、18 B、26 C、34 D、46

查看试题解析

二、填空题（每小题3分，共18分）

11. 计算： $\sqrt{9}$ = ．

查看试题解析
12. 已知 $- \frac{1}{2} x^{n} y^{2}$ 与^{$x^{3} y^{m}$}是同类项，则^{$m^{n}$}＝．

查看试题解析
13. 已知：数轴上一个点到﹣2的距离为5，则这个点表示的数是

查看试题解析
14. 若一个正数的平方根是3a-2和5，则这个正数是．

查看试题解析
15. 我们定义一个新运算“★”如下：x≤y时，x★y＝x²；x＞y时，x★y＝y．则当z＝-3时，代数式（-2★z）-（-4★z）的值为．

查看试题解析
16. 任何实数 $a$ ，可用[ $a$ ]表示不超过 $a$ 的最大整数，如[4]＝4，[ $\sqrt{3}$ ]＝1．现对87进行如下操作：87 $\overset{第一次}{\to}$ [ $\sqrt{87}$ ]＝9 $\overset{第二次}{\to}$ [ $\sqrt{9}$ ]＝3 $\overset{第三次}{\to}$ [ $\sqrt{3}$ ]＝1，这样对87只需进行3次操作后变为1，类似的：（1）对15只需进行次操作后变为1；（2）只需进行4次操作后变为1的所有正整数中，最大的是．

查看试题解析

三、解答题（52分）

17. 计算：

(1)、 $（ - \frac{1}{2} + \frac{3}{4} - \frac{2}{3} ） \times 12$

(2)、 $- 1^{2022} + （ - 3 ）^{2} \div \frac{1}{2} - | - 2 |$

查看试题解析
18. 在数轴上表示下列各数，并把这些数按从小到大顺序进行排列，用“＜”连接： $\sqrt{4}$ ， -（-3）， $- 3 \frac{1}{2}$ ， -1.5．

查看试题解析
19.

(1)、先化简，再求值：， $2 （ a^{2} + a b) - 3 （ \frac{2}{3} a^{2} - a b ）$ 其中 $a = 2 ， b = - 3$

(2)、已知 $2 x + y = 3$ ，求代数式 $3 (x - 2 y) + 5 (x + 2 y - 1) - 2$ 的值．

查看试题解析

20. 目前，我国新冠肺炎疫情防控已进入常态化阶段，截至2020年10月31日24时，据31个省（自治区、直辖市）和新疆生产建设兵团报告，现有确诊病例429例，下表是2020年11月1日至11月7日的当日新增确诊病例和当日新增治愈病例．（统计数据都以当日24时为界）

日期	1日	2日	3日	4日	5日	6日	7日
当日新增确诊病例	24	34	17	28	33	28	31
当日新增治愈病例	20	30	16	30	36	37	45

(1)、请问到11月2日24时止，现有病例是多少例？

(2)、请问到几月几日24时止，病例最多？

(3)、若治愈一位新冠肺炎病人需要a元，那么11月1日0时至11月7日24时治愈的肺炎病人共需要多少元钱？

查看试题解析

21. 老王想靠着一面足够长的旧墙EF，开垦一块长方形的菜地ABCD，如图所示，菜地的一边靠墙，另外三边用竹篱笆围起来，并在平行于墙的一边BC上留1米宽装门，已知现有竹篱笆长共32米．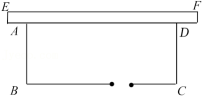

(1)、设垂直于墙面的一边AB长为 $x$ 米，则AD边的长用含 $x$ 的代数式可表示为米．

(2)、设菜地面积为S，用含 $x$ 的代数式来表示S．

(3)、当 $x$ ＝8时，菜地面积为多少平方米？

查看试题解析
22. 阅读材料，解答下面的问题：
∵ $\sqrt{4}$ ＜ $\sqrt{7}$ ＜ $\sqrt{9}$ ，即2＜ $\sqrt{7}$ ＜3，

∴ $\sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7}$ ﹣2.

(1)、求 $\sqrt{6}$ 的整数部分.

(2)、已知5+ $\sqrt{6}$ 的小数部分是a，5﹣ $\sqrt{6}$ 的小数部分是b，求（a+b）²⁰²¹的值.

查看试题解析
23. 某品牌饮水机生产一种饮水机和饮水机桶，饮水机每台定价350元，饮水机桶每只定价50元，厂方开展促销活动期间，可以同时向客户提供两种优惠方案：（1）买一台饮水机送一只饮水机桶；（2）饮水机和饮水机桶都按定价的90%付款。现某客户到该饮水机厂购买饮水机30台，饮水机桶x只（x超过30）．

(1)、若该客户按方案（1）购买，求客户需付款（用含x的式子表示）；

(2)、若该客户按方案（2）购买，求客户需付款（用含x的式子表示）；

(3)、当x＝40时，哪一种促销方案更优惠？

查看试题解析
24. 若数轴上的点A、点B表示的数分别为 $a ， b$ ，则A、B两点之间的距离AB＝|a-b|，线段AB的中点表示的数为 $\frac{a + b}{2}$ ．
解决问题：现数轴上有一点A表示的数为-10，点B表示的数为18，点P从点A出发，以每秒2个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒1个单位长度的速度向左匀速运动，设运动时间为t秒（t＞0）．

(1)、①A、B两点之间的距离AB＝，线段AB的中点表示的数为． ②当t＝时，P、Q两点相遇，相遇点所表示的数为．

(2)、求当t为何值时，PQ＝ $\frac{1}{2}$ AB．

(3)、折叠数轴使点A、P重合，折点记为M，还原后再折叠数轴使点B、P重合，折点记为N，点P在运动过程中，M、N两点间的距离是否发生变化？若变化，请说明理由；若不变，请求出线段MN的长度．

查看试题解析