浙江省义乌市三校联考2022-2023学年八年级上学期数学期中试卷
试卷更新日期:2022-12-02 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 在以下“绿色食品”、“节能减排”、“循环回收”、“质量安全”四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式 的解集在数轴上表示正确的是( )A、
2. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,∠B=60°,∠ACD=100°,那么∠A=( )
3. 如图,∠B=60°,∠ACD=100°,那么∠A=( ) A、30° B、40° C、50° D、60°4. 若 , 则下列各式中一定成立的是( )A、 B、 C、 D、5. 下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例是( )A、两个角分别为13°,45° B、两个角分别为40°,45° C、两个角分别为45°,45° D、两个角分别为105°,45°6. 如图,点 , 分别在 , 上,与相交于点 , 已知 , 现添加下面的哪一个条件后,仍不能判定≌的是( )
A、30° B、40° C、50° D、60°4. 若 , 则下列各式中一定成立的是( )A、 B、 C、 D、5. 下列选项中,可以用来说明命题“两个锐角的和是锐角”是假命题的反例是( )A、两个角分别为13°,45° B、两个角分别为40°,45° C、两个角分别为45°,45° D、两个角分别为105°,45°6. 如图,点 , 分别在 , 上,与相交于点 , 已知 , 现添加下面的哪一个条件后,仍不能判定≌的是( )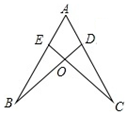 A、 B、 C、 D、7. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( )
A、 B、 C、 D、7. 如图,在中, , 分别以点,点为圆心以大于为半径画弧,两弧交于 , , 连接交于点 , 连接 , 以为圆心,长为半径作弧,交于点,则:( ) A、1: B、1:2 C、1: D、1:8. 如图,在的正方形网格中,点 , 在格点上,要找一个格点 , 使是等腰三角形是其中一腰 , 则图中符合条件的格点有( )
A、1: B、1:2 C、1: D、1:8. 如图,在的正方形网格中,点 , 在格点上,要找一个格点 , 使是等腰三角形是其中一腰 , 则图中符合条件的格点有( ) A、2个 B、3个 C、4个 D、5个9. 已知不等式的负整数解恰好是-3,-2,-1,那么满足条件( )A、 B、 C、 D、10. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:≌;;;;其中正确的说法有( )
A、2个 B、3个 C、4个 D、5个9. 已知不等式的负整数解恰好是-3,-2,-1,那么满足条件( )A、 B、 C、 D、10. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:≌;;;;其中正确的说法有( )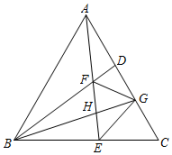 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(每题4分,共24分)
-
11. 用不等式表示“的2倍小于3”为 .12. 等腰三角形的顶角的度数是50°,则底角的度数是度.13. ”两个全等的三角形的周长相等“的逆命题是命题。(填”真“或”假“)。14. 若不等式的解集为 , 则的值是 .15. 如图,在中, , , , 点在边上, , , 垂足为 , 与交于点 , 则的长是 .
 16. 图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚米,米,为上固定连接点,靠背米.档位为Ⅰ档时, , 档位为Ⅱ档时,当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端向后靠的水平距离即为米.
16. 图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚米,米,为上固定连接点,靠背米.档位为Ⅰ档时, , 档位为Ⅱ档时,当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端向后靠的水平距离即为米.
三、解答题(共66分)
-
17. 解下列不等式(1)、 ;(2)、18. 如图, , , , 说出的理由.

解: ,
, 即 .
在和中,
,
19. 如图,在正方形网格上有一个 . (1)、若网格上的每个小正方形的边长为1,则的面积为 .(2)、在直线上找一点 , 使最短.20. 如图,在等边三角形中,点 , 分别在边 , 上,且 , 过点作 , 交的延长线于点 .
(1)、若网格上的每个小正方形的边长为1,则的面积为 .(2)、在直线上找一点 , 使最短.20. 如图,在等边三角形中,点 , 分别在边 , 上,且 , 过点作 , 交的延长线于点 .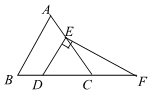 (1)、求证:是等腰三角形;(2)、若 , 求的长.21. 如图,于 , 于 , 若 , .
(1)、求证:是等腰三角形;(2)、若 , 求的长.21. 如图,于 , 于 , 若 , . (1)、求证:≌;(2)、已知 , , 求的长.22. 如图,中, , 垂直平分 , 交于点 , 交于点 , 且 .
(1)、求证:≌;(2)、已知 , , 求的长.22. 如图,中, , 垂直平分 , 交于点 , 交于点 , 且 . (1)、求证:(2)、求证:BD=DE(3)、若 , , 求的周长.23. 如图:
(1)、求证:(2)、求证:BD=DE(3)、若 , , 求的周长.23. 如图: (1)、问题发现:如图1,与均为等腰直角三角形, , 写出线段、的数量关系为和位置关系 , 请说明理由.(2)、深入探究:在(1)的条件下,若点 , , 在同一直线上,为中边上的高,请直接写出线段 , , 之间的数量关系 .(3)、解决问题:如图3,已知中, , , , 以为直角边作等腰直角 , , , 连接 , 则的长为 .24. 已知中 .
(1)、问题发现:如图1,与均为等腰直角三角形, , 写出线段、的数量关系为和位置关系 , 请说明理由.(2)、深入探究:在(1)的条件下,若点 , , 在同一直线上,为中边上的高,请直接写出线段 , , 之间的数量关系 .(3)、解决问题:如图3,已知中, , , , 以为直角边作等腰直角 , , , 连接 , 则的长为 .24. 已知中 . (1)、如图1、2,若点是上一点,且 , 点是上的动点,将沿对折,点的对应点为(点和点 在直线 的异侧),与交于点 .
(1)、如图1、2,若点是上一点,且 , 点是上的动点,将沿对折,点的对应点为(点和点 在直线 的异侧),与交于点 .①当时,求的度数.
②当是等腰三角形时,求的度数.
(2)、如图3,若点是上一点,且 , 是线段上的动点,以为直角构造等腰直角(三点顺时针方向排列),在点的运动过程中,直接写出的最小值.