浙江省温州市瑞安东北部(龙湾西南部)十一校2022-2023学年九年级上学期数学第二次联考试卷
试卷更新日期:2022-12-02 类型:期中考试
一、选择题(本题有10小题,每小题4分,共40分.)
-
1. 下列事件中属于必然事件的是( )A、一个奇数与一个偶数的和为奇数 B、一个三角形三个内角的和小于180° C、任意抛一枚均匀的硬币,正面朝上 D、有一匹马奔跑的速度是70米/秒2. 已知⊙O的直径长为4,点A,B在⊙O上,则AB的长不可能是( )A、2 B、3 C、4 D、83. 已知抛物线的开口向下,则a的值可能为( )A、-2 B、 C、1 D、4. 若 , 则a=( )A、 B、1 C、2 D、35. 把抛物线y=3x2向右平移2个单位,再向下平移4个单位,得到的抛物线的表达式为( )A、y=3(x-2)2+4 B、y=3(x-2)2-4 C、y=3(x+2)2-4 D、y=3(x+2)2+46. 如图,四边形ABCD内接于⊙O,点E为上一点,连结BE,DE.若∠A+∠ABC+∠ADC=240°,则∠E( )
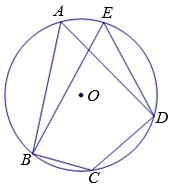 A、55° B、60° C、65° D、70°7. 如图,l1 , l2 , l3 , l4是一组平行线,l5 , l6与这组平行线依次相交于点A,B,C,D和E,F,G,H.若AB∶BC∶CD=2∶3∶4,EG=10,则EH的长为( )
A、55° B、60° C、65° D、70°7. 如图,l1 , l2 , l3 , l4是一组平行线,l5 , l6与这组平行线依次相交于点A,B,C,D和E,F,G,H.若AB∶BC∶CD=2∶3∶4,EG=10,则EH的长为( )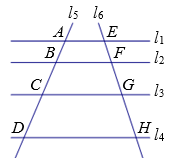 A、14 B、16 C、18 D、208. 已知点A( , y1),B(-3,y2),C(1,y3)均在抛物线y=x2+4x+m上,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1<y3<y2 C、y1<y2<y3 D、y1>y3>y29. 如图,用六个全等的直角三角形恰好拼成一大一小两个正六边形,则大正六边形与小正六边形的周长之比为( )
A、14 B、16 C、18 D、208. 已知点A( , y1),B(-3,y2),C(1,y3)均在抛物线y=x2+4x+m上,则y1 , y2 , y3的大小关系是( )A、y1>y2>y3 B、y1<y3<y2 C、y1<y2<y3 D、y1>y3>y29. 如图,用六个全等的直角三角形恰好拼成一大一小两个正六边形,则大正六边形与小正六边形的周长之比为( )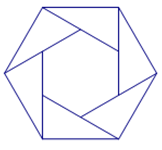 A、 B、 C、2 D、310. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.点P,Q分别为AB,GH的中点,若PQ恰好经过点F,则的值为( )
A、 B、 C、2 D、310. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.点P,Q分别为AB,GH的中点,若PQ恰好经过点F,则的值为( )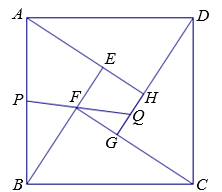 A、 B、3 C、 D、4
A、 B、3 C、 D、4二、填空题(本题有6小题,每小题5分,共30分)
-
11. 二次函数y=x2-4x+2的图象与y轴的交点坐标为 .12. 有5张卡片,每张卡片分别写有不同的从1到5的自然数.从中任意抽出一张卡片,卡片上的数是5的概率是 .13. 已知圆的半径为9 cm,圆弧的度数为120°,则弧长为cm.14. 如图,B船位于A船正东方向5 km处.现在A船以2 km/h的速度朝正北方向行驶,同时B船以1 km/h的速度朝正西方向行驶,当两船相距最近时,行驶了h.
 15. 如图,⊙O是△ABC的外接圆,∠ACB=45°,CD⊥AB于点D,延长CD交⊙O于点E,若点O到AB,CD的距离分别为5,3,则BD的长为 .
15. 如图,⊙O是△ABC的外接圆,∠ACB=45°,CD⊥AB于点D,延长CD交⊙O于点E,若点O到AB,CD的距离分别为5,3,则BD的长为 . 16. 如图是某路灯的示意图,立柱OE与水平地面垂直,两盏路灯挂在灯杆OE的异侧(灯臂AB,CD近似看作线段,AB、CD),AE⊥OE,∠ABO=∠DCO=120°.小丽(身高1.5米)站在点P处时,点F,D,E在同一直线上,向后移动4.5米到达点Q,点G,D,B,A在同一直线上.测得OP=6米,则OE=米,AB=米.
16. 如图是某路灯的示意图,立柱OE与水平地面垂直,两盏路灯挂在灯杆OE的异侧(灯臂AB,CD近似看作线段,AB、CD),AE⊥OE,∠ABO=∠DCO=120°.小丽(身高1.5米)站在点P处时,点F,D,E在同一直线上,向后移动4.5米到达点Q,点G,D,B,A在同一直线上.测得OP=6米,则OE=米,AB=米.
三、解答题(本题有8个小题,共80分。)
-
17. 已知抛物线的表达式为y=x2-2x-3.(1)、求抛物线的顶点坐标.(2)、当0≤x≤3时,求y的取值范围.18. 一个箱子里有1个红球、1个白球,它们除颜色外其余均相同.从箱子里先摸出一个球,放回去摇匀后,再摸出一个球.(1)、有人说,两次摸球只有3种可能的结果:2红、2白、1红1白,所以两次都摸到红球的概率应该是 , 这种说法正确吗?请判断并说明理由.(2)、往箱子中再放入n个红球,2个白球,它们除颜色外其余均相同,从箱子中任意摸一个球,若摸到红球的概率为0.8,求n的值.19. 如图,在矩形ABCD中,E为AD上一点,连结AC,BE交于点F,FG⊥CD于G.
 (1)、求证: .(2)、若AE=DE=3,求FG的长.20. 如图,在6×8的方格纸中,点A,B,C均为格点,请按要求在方格纸内作图.
(1)、求证: .(2)、若AE=DE=3,求FG的长.20. 如图,在6×8的方格纸中,点A,B,C均为格点,请按要求在方格纸内作图. (1)、在图1中作出与△ABC相似的格点△CDE.(2)、在图2中作出与∠C相等的∠AFB,点F为格点且不与点C重合.21. 已知抛物线y=-x2+bx+c经过点A(0,1),B(4,1).(1)、求抛物线的函数表达式.(2)、点C(m,n)在抛物线上且在第一象限.设点C到AB的距离为d,若3<d≤4,求m的取值范围.22. 如图,四边形ABCD为⊙O的内接四边形, AB为⊙O的直径,作DE⊥AB于点E,交AC于点F,其中 .
(1)、在图1中作出与△ABC相似的格点△CDE.(2)、在图2中作出与∠C相等的∠AFB,点F为格点且不与点C重合.21. 已知抛物线y=-x2+bx+c经过点A(0,1),B(4,1).(1)、求抛物线的函数表达式.(2)、点C(m,n)在抛物线上且在第一象限.设点C到AB的距离为d,若3<d≤4,求m的取值范围.22. 如图,四边形ABCD为⊙O的内接四边形, AB为⊙O的直径,作DE⊥AB于点E,交AC于点F,其中 . (1)、求证:△ABC∽△DAE.(2)、当AD= , BE=4时,求CD的长.23. 根据以下素材,探索完成任务.
(1)、求证:△ABC∽△DAE.(2)、当AD= , BE=4时,求CD的长.23. 根据以下素材,探索完成任务.如何设计喷水池喷头的安装方案?
素材1
图1中有一个直径为20 m的圆形喷水池,四周安装一圈喷头,喷射水柱呈抛物线型,在水池中心O处立着一个直径为1 m的圆柱形实心石柱,各方向喷出的水柱在石柱顶部的中心点M处汇合,如图2,水柱距水池中心4 m处到达最高,高度为6 m.


素材2
如图3,拟在水池里过水池中心的直线上安装一排直线型喷头(喷射水柱竖直向上,高度均为m);相邻两个直线型喷头的间距均为1.2 m,且喷射的水柱不能碰到抛物线型水柱,要求在符合条件处都安装喷头,安装后关于OM成轴对称分布.

问题解决
任务1
确定水柱形状
在图2中建立合适的直角坐标系,任选一条抛物线求函数表达式.
任务2
确定石柱高度
在你所建立的坐标系中,确定水柱汇合点M的纵坐标.
任务3
拟定设计方案
请给出符合所有要求的直线型喷头的安装数量,并根据你所建立的直角坐标系,求出离中心O最远的两个直线型喷头的坐标.
24. 如图1,在Rt△ABC中,∠C=90°,BC=3,AB=5,点P为AC上一点,PD⊥AB于点D,连结PB,以PD为直径的圆交BP于点E,交AC于点F,连结DE,DF,EF. (1)、求证:∠DEF=∠ABC.(2)、当△DEF为等腰三角形时,求所有满足条件的AP的长.(3)、如图2,过D作DM∥EF交PB于点M,若点M为PB的中点,则DM . (直接写出答案)
(1)、求证:∠DEF=∠ABC.(2)、当△DEF为等腰三角形时,求所有满足条件的AP的长.(3)、如图2,过D作DM∥EF交PB于点M,若点M为PB的中点,则DM . (直接写出答案)