浙江省嘉兴市桐乡六中教育集团三校联考2022-2023学年七年级上学期期中数学试卷

试卷更新日期：2022-12-02 类型：期中考试

进入出卷网下载

一、选择题（每小题有4个选项，其中有且只有一个正确，每小题3分，共30分）

1. -8的相反数是（）

A、-8 B、8 C、 $- \frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
2. 2022年2月5日，嘉兴某区最高气温 $7^{°} C$ ，最低气温为 $- 2^{°} C$ ，那么这天的最高气温比最低气温高 $($ $)$

A、 $9^{°} C$ B、 $- 9^{°} C$ C、 $5^{°} C$ D、 $- 5^{°} C$

查看试题解析
3. 下列四个数中，最小的是 $($ $)$

A、 $| - 1.5 |$ B、0 C、 $- (- 3)$ D、-3

查看试题解析
4. 第七次全国人口普查数据显示，嘉兴市常住人口约为540万人，540万用科学记数法表示为 $($ $)$

A、 $5.4 \times 10^{2}$ B、 $0.54 \times 10^{3}$ C、 $5.4 \times 10^{6}$ D、 $0.54 \times 10^{7}$

查看试题解析
5. 实数 $\sqrt{7}$ 的整数部分是 $($ $)$

A、1 B、2 C、3 D、4

查看试题解析
6. 用代数式表示“ $a$ 与 $b$ 的平方的差”正确的是 $($ $)$

A、 $a^{2} - b^{2}$ B、 ${(a - b)}^{2}$ C、 $a - b^{2}$ D、 $a^{2} - b$

查看试题解析
7. 代数式 $- 4 π a b^{2}$ 的系数与次数分别是 $($ $)$

A、 $- 4 π$ ， 3 B、 $- 4 π$ ， 4 C、-4，3 D、-4，4

查看试题解析
8. 平方根等于本身的数是 $($ $)$

A、-1 B、0 C、1 D、0，±1

查看试题解析
9. 数轴上点 $A$ ， $B$ ， $C$ 分别表示数 $- 1$ ， $m$ ， $- 1 + m$ ，下列说法正确的是 $($ $)$

A、点 $C$ 一定在点 $A$ 的右边 B、点 $C$ 一定在点 $A$ 的左边 C、点 $C$ 一定在点 $B$ 的右边 D、点 $C$ 一定在点 $B$ 的左边

查看试题解析
10. 已知 $a$ ， $b$ 为实数，下列说法：①若 $a b < 0$ ，且 $a$ ， $b$ 互为相反数，则 $\frac{a}{b} = - 1$ ；②若 $| a - b | + a - b = 0$ ，则 $a - b = 0$ ；③若 $a < b$ ， $a b < 0$ 且 $| a | < | b |$ ，则 $a + b < 0$ ；④若 $a + b < 0$ ， $a b > 0$ ，则 $| - 2 a - 3 b | = 2 a + 3 b$ ；⑤若 $| a | > | b |$ ，则 $(a + b) (a - b) < 0$ ，其中正确个数为 $($ $)$

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本题有6小题，每小题3分，共18分）

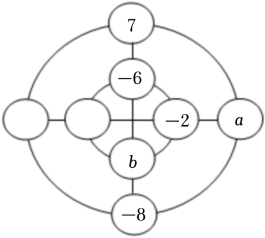
11. 如果盈利100元记作+100元，那么亏损50元记作元.

查看试题解析
12. 比较大小： $| - 5 |$ 2.

查看试题解析
13. 由四舍五入得到的近似数83.50，精确到位.

查看试题解析
14. 已知 $x - y + 5 = 0$ ， $x y = 2$ ，则代数式 $x - y - x y$ 的值为 .

查看试题解析
15. 若 $m^{2} = {(- \sqrt{3})}^{2}$ ，则 $m =$ .

查看试题解析
16. 爱动脑筋的小明同学设计了一种“幻圆”游戏，将1，-2，3，-4，5，-6，7，-8分别填入图中的圆圈内，使横、竖以及内外两圈上的4个数字之和都相等，他已经将-2，-6，7，-8这四个数填入了圆圈，则图中 $a - b$ 的值为 .

查看试题解析

三、解答题（第17～22题，每题6分，第23、24题，每题8分，共52分）

17. 计算：

(1)、 $5 - (- 8)$ ；

(2)、 $- 2^{2} \times \sqrt{9} \div \sqrt[3]{64} - {(- 1)}^{2022}$ .

查看试题解析
18. 下面是亮亮同学计算一道题的过程：
$15 \div 5 \times (- 3) - 6 \times (\frac{3}{2} + \frac{2}{3})$

$= 15 \div (- 15) - 6 \times \frac{3}{2} + 6 \times \frac{2}{3} \dots \dots$ ①

$= - 1 - 9 + 4 \dots \dots$ ②

$= - 6 \dots \dots$ ③

(1)、亮亮计算过程从第步出现错误的；（填序号）

(2)、请你写出正确的计算过程.

查看试题解析
19. 将下列各数写到相应的横线上，（填序号）
① ${(- \sqrt{2})}^{2}$ ；② $\sqrt[3]{9}$ ；③ $\frac{22}{7}$ ；④ $- \frac{π}{2}$ ；⑤ $- | - 3 |$ ；⑥ $- 4^{2}$ .

(1)、有理数： ${$     $\dots}$ ；

(2)、无理数： ${$     $\dots}$ ；

(3)、负数： ${$     $\dots}$ .

查看试题解析
20. 一只蚂蚁从点 $P$ 出发，在一条水平直线上来回匀速爬行.记向右爬行的路程为正，向左爬行的路程为负，爬行的路程依次为（单位：厘米）+7，-6，-5，-6，+13，-3.

(1)、请通过计算说明蚂蚁最后是否回到了起点 $P$ .

(2)、若蚂蚁爬行的速度是0.5厘米 $/$ 秒，问蚂蚁共爬行了多少时间？

查看试题解析
21. 如图，一个长方形运动场被分割成 $A$ ， $B$ ， $A$ ， $B$ ， $C$ 共5个区， $A$ 区是边为 $a$ 米的正方形， $C$ 区是边长为 $c$ 米的正方形.

(1)、 $B$ 区相邻两边的长度分别为米，米.（用含 $a$ ， $c$ 的代数式表示）

(2)、如果 $a = 20$ 米， $c = 10$ 米，求整个长方形运动场的面积.

查看试题解析
22. 观察下列各式：
① $\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ；② $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ；③ $\frac{1}{\sqrt{4} + \sqrt{3}} = \sqrt{4} - \sqrt{3} \dots$

(1)、请根据以上规律，写出第4个式子：.

(2)、请根据以上规律，写出第 $n$ 个式子：.

(3)、根据以上规律计算下列式子的值： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{2022} + \sqrt{2021}}$ .

查看试题解析
23. 小明在做浙教版七上课本第75页第6题：“利用如图 $4 \times 4$ 方格（每个方格边长为 $1)$ ，作出面积为8的正方形”时，发现利用分割正方形的方法，可以作出面积为8的正方形（如图1阴影部分），进一步开展探究活动：

【探究1】图1中正方形边长为▲ .

【探究2】仿照上述作法，小明又作出一个正方形（如图2阴影部分），则该正方形面积为▲ ，边长为 ▲ .

【探究3】如图3，是 $5 \times 5$ 方格（每个方格边长为 $1)$ ，仿照上述作法，请你画出一个面积为13的正方形.

查看试题解析
24. 阅读材料：若点 $M$ ， $N$ 在数轴上分别表示实数 $m$ ， $n$ ，那么 $M$ ， $N$ 之间的距离可表示为 $| m - n |$ .例如 $| 3 - 1 |$ ，即表示3，1在数轴上对应的两点之间的距离；同样： $| 5 + 3 | = | 5 - (- 3) |$ 表示5， $- 3$ 在数轴上对应的两点之间的距离.根据以上信息，完成下列题目：

(1)、已知 $A$ ， $B$ ， $C$ 为数轴上三点，点 $A$ 对应的数为 $\sqrt{2}$ ，点 $C$ 对应的数为1.
①若点 $B$ 对应的数为 $- 2$ ，则 $B$ ， $C$ 两点之间的距离为；

②若点 $A$ 到点 $B$ 的距离与点 $A$ 到点 $C$ 的距离相等，则点 $B$ 对应的数是 .

(2)、对于 $| x - 3 | + | x + 4 |$ 这个代数式.
①它的最小值为；

②若 $| x - 3 | + | x + 4 | + | y - 1 | + | y + 2 | = 10$ ，则 $x + y$ 的最大值为 .

查看试题解析