浙江省温州市瑞安市五校联考2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-12-02 类型:期末考试
一、单选题
-
1. 平面内有两点P,O,⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )A、圆内 B、圆上 C、圆外 D、圆上或圆外2. 已知 , 则的值为( )A、 B、 C、 D、3. 把抛物线 先向右平移1个单位,再向上平移n个单位后,得到抛物线 ,则n的值是( )A、1 B、2 C、3 D、44. 一个不透明的布袋里装有6个只有颜色不同的球,其中1个黑球、2个白球、3个红球,从布袋里任意摸出1个球,是白球的概率为( )A、 B、 C、 D、5. 如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )
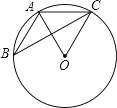 A、30° B、45° C、60° D、70°6. 如图,在△ABC中, , 则下列等式不成立的是( )
A、30° B、45° C、60° D、70°6. 如图,在△ABC中, , 则下列等式不成立的是( )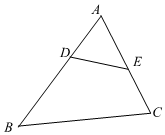 A、 B、 C、 D、7. 如图,在△ABC中,AB=AC,D是BC中点,将△ADC绕点A逆时针旋转90°得△AEF,点D,C分别对应点E,F,连接CF.若∠BAC=62°,则∠CFE等于( )
A、 B、 C、 D、7. 如图,在△ABC中,AB=AC,D是BC中点,将△ADC绕点A逆时针旋转90°得△AEF,点D,C分别对应点E,F,连接CF.若∠BAC=62°,则∠CFE等于( )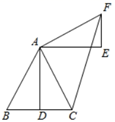 A、14° B、15° C、16° D、17°8. 二次函数 y=-x2+2x+4,当x时,则y的取值范围为( )A、 B、 C、 D、9. 如图,⊙O是正△ABC的外接圆,△DOE是顶角为120°的等腰三角形,点O与圆心重合,点D,E分别在圆弧上,若⊙O的半径是6,则图中阴影部分的面积是( )
A、14° B、15° C、16° D、17°8. 二次函数 y=-x2+2x+4,当x时,则y的取值范围为( )A、 B、 C、 D、9. 如图,⊙O是正△ABC的外接圆,△DOE是顶角为120°的等腰三角形,点O与圆心重合,点D,E分别在圆弧上,若⊙O的半径是6,则图中阴影部分的面积是( ) A、 B、9 C、 D、 910. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,过点G作GD的垂线交AB于点I,若 , 则的值为( )
A、 B、9 C、 D、 910. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示,过点G作GD的垂线交AB于点I,若 , 则的值为( )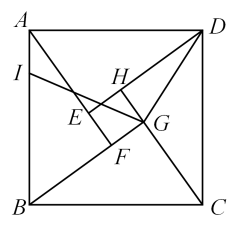 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
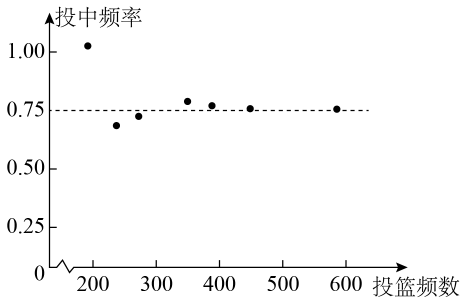
11. 抛物线 y=x2+1与y轴的交点坐标是.12. 一名职业篮球球员某次投篮训练结果记录如图所示,由此可估计这名球员投篮800次,投中的次数约为次.
 13. 已知扇形的圆心角为 ,半径为2,则该扇形的弧长为 .14. 如图,AD是⊙O的直径,于E,若DE=3,BC=8,则⊙O的半径为.
13. 已知扇形的圆心角为 ,半径为2,则该扇形的弧长为 .14. 如图,AD是⊙O的直径,于E,若DE=3,BC=8,则⊙O的半径为. 15. 如图,在平面直角坐标系中,点A,B的坐标分别是A(2,2),B(5,5),若二次函数与y=ax2+bx+c的图象经过A,B两点,且该函数图象的顶点为不与A,B重合的点M(x,y),其中x,y是整数,且1<x<7,1<y<7,则a的值为.
15. 如图,在平面直角坐标系中,点A,B的坐标分别是A(2,2),B(5,5),若二次函数与y=ax2+bx+c的图象经过A,B两点,且该函数图象的顶点为不与A,B重合的点M(x,y),其中x,y是整数,且1<x<7,1<y<7,则a的值为.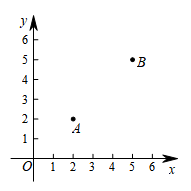 16. 如图是一款上铺的收纳挂篮(如图1),其侧截面可看作直角梯形,现有一长方体形状的物体放置在该挂篮中,当物体如图2放置时,AB∥PQ,正方形DMEC为露出挂篮部分,此时 , 当物体如图3放置时,与Q重合,四边形为露出挂篮部分,此时 , 且 , 则到PQ的距离为.
16. 如图是一款上铺的收纳挂篮(如图1),其侧截面可看作直角梯形,现有一长方体形状的物体放置在该挂篮中,当物体如图2放置时,AB∥PQ,正方形DMEC为露出挂篮部分,此时 , 当物体如图3放置时,与Q重合,四边形为露出挂篮部分,此时 , 且 , 则到PQ的距离为.
三、解答题
-
17. 如图,△ABC分别交⊙O于点A,B,D,E,且CA=CB.求证:AD=BE.
 18. 一个不透明的口袋中装有三个除所标数字外完全相同的小球,小球上分别标有数字-1,0,1,小丽先从袋中随机取出一个小球,记录下小球上的数字为x,不放回,再从袋中随机取出一个小球,记录下小球上的数字为y,设点M的坐标为(x,y).(1)、请用树状图法或列表法表示出点M坐标的所有情况;(2)、求点M(x,y)的横坐标与纵坐标之和结果不小于0的概率.19. 如图,在Rt△ABC中, , 点D是AB的中点,DE∥BC,BE⊥AB.
18. 一个不透明的口袋中装有三个除所标数字外完全相同的小球,小球上分别标有数字-1,0,1,小丽先从袋中随机取出一个小球,记录下小球上的数字为x,不放回,再从袋中随机取出一个小球,记录下小球上的数字为y,设点M的坐标为(x,y).(1)、请用树状图法或列表法表示出点M坐标的所有情况;(2)、求点M(x,y)的横坐标与纵坐标之和结果不小于0的概率.19. 如图,在Rt△ABC中, , 点D是AB的中点,DE∥BC,BE⊥AB. (1)、求证:;(2)、若 , 求的值.20. 如图是的正方形网格,已知△ABC,请按下列要求完成作图(要求保留作图痕迹,不要求写作法和结论)
(1)、求证:;(2)、若 , 求的值.20. 如图是的正方形网格,已知△ABC,请按下列要求完成作图(要求保留作图痕迹,不要求写作法和结论) (1)、将△ABC绕C点按顺时针方向旋转 , 得到 , 请在图1中作出;(2)、在图2中,在AC所在直线的左侧画∠AEC,使得;(3)、在图3中,仅用无刻度直尺在线段AC上找一点M,使得.21. 如图,y=ax2-2ax+a-4与x轴负半轴交于A,交y轴于B,过抛物线顶点C作轴,垂足为D,四边形AOCD是平行四边形.
(1)、将△ABC绕C点按顺时针方向旋转 , 得到 , 请在图1中作出;(2)、在图2中,在AC所在直线的左侧画∠AEC,使得;(3)、在图3中,仅用无刻度直尺在线段AC上找一点M,使得.21. 如图,y=ax2-2ax+a-4与x轴负半轴交于A,交y轴于B,过抛物线顶点C作轴,垂足为D,四边形AOCD是平行四边形. (1)、求抛物线的对称轴以及二次函数的解析式;(2)、作轴交抛物线于另一点E,交OC于F,求EF的长;(3)、该二次函数图象上有一点G(m,n)若点G到y轴的距离小于2,则n的取值范围为.22. 如图,在Rt△ABC中, , D是BC上一点,连接AD,△ACD的外接圆⊙O交AB于点E,点F是上一点,且 , 连接AF,OF.
(1)、求抛物线的对称轴以及二次函数的解析式;(2)、作轴交抛物线于另一点E,交OC于F,求EF的长;(3)、该二次函数图象上有一点G(m,n)若点G到y轴的距离小于2,则n的取值范围为.22. 如图,在Rt△ABC中, , D是BC上一点,连接AD,△ACD的外接圆⊙O交AB于点E,点F是上一点,且 , 连接AF,OF.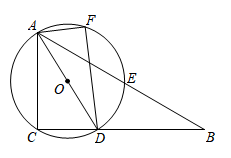 (1)、求证:.(2)、当E为AB中点时, , 求BC的长度.23. 冬至吃汤圆是我国南方的一项传统民俗,既代表着团圆,又寓意着添岁.为了迎接冬至的来临,瑞安市某商家向广大市民出售肉馅汤圆,已知该汤圆的成本价为20元/盒,经调查发现:在一段时间内,该商品的日销售量y(盒)与售价x(元/盒)成一次函数关系.其对应关系如下表:
(1)、求证:.(2)、当E为AB中点时, , 求BC的长度.23. 冬至吃汤圆是我国南方的一项传统民俗,既代表着团圆,又寓意着添岁.为了迎接冬至的来临,瑞安市某商家向广大市民出售肉馅汤圆,已知该汤圆的成本价为20元/盒,经调查发现:在一段时间内,该商品的日销售量y(盒)与售价x(元/盒)成一次函数关系.其对应关系如下表:售价(元/盒)
25
30
35
日销售量(盒)
110
a
90
(1)、根据以上信息,填空:表中a的值是 , y关于x的函数关系式是;(2)、若根据市场的定价规则,该汤圆的售价不得高于40元/盒,求售价为多少时,日销售利润w最大,最大利润是多少?(3)、在(1)的条件下,为了增加店铺的人气,商家决定搞促销活动.顾客每购买一盒肉馅汤圆可以获得m元的现金奖励 , 商家想在日销售量不少于60盒的基础上,日销售最大利润为1650元,求出此时m的值.24. 如图1,在菱形ABCD中,∠B为锐角,点P,H分别在边AD,CB上,且 , 在AB边上取点M,N(点N在BM之间)使AM=5BN,点P从点D匀速运动到点A时,点Q恰好从点M匀速运动到点N,连结PQ,PH分别交对角线AC于E,F,记QN=x,QP=y,已知. (1)、①请判断PF与FH的大小关系,并说明理由;
(1)、①请判断PF与FH的大小关系,并说明理由;②求AD,BN的长;
(2)、如图2,连结QF,当四边形FQBH中有两边平行时,求AE∶EC的值;(3)、若 , 连结QH,求△FQH面积的最小值.