浙江省温州市乐清市七校2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-12-02 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\frac{b}{a} = \frac{3}{4}$ ，则 $\frac{a + b}{a}$ ＝（　　）

A、 $\frac{7}{4}$ B、 $\frac{4}{7}$ C、 $\frac{1}{4}$ D、 $\frac{4}{3}$

查看试题解析
2. 下列事件中，属于不可能事件的是（）

A、a是实数，则 $| a | \geq 0$ B、一匹马奔跑的速度是每秒100米 C、任意一个三角形都有外接圆 D、抛掷一枚骰子，朝上面的点数是6

查看试题解析
3. 将抛物线 $y = - x^{2}$ 向左平移 $3$ 个单位，再向上平移 $5$ 个单位，则平移后的抛物线解析式为（）

A、 $y = - {(x + 3)}^{2} + 5$ B、 $y = - {(x + 3)}^{2} - 5$ C、 $y = - {(x - 3)}^{2} + 5$ D、 $y = - {(x - 3)}^{2} - 5$

查看试题解析
4. 如图，已知A，B均为⊙O上一点，若∠AOB＝80°，则∠ACB＝（　　）

A、80° B、70° C、60° D、40°

查看试题解析
5. 如图，FG $∥$ DE $∥$ BC，若BD=4，DF=3，CE=3，则GE的长为（）

A、2 B、4 C、 $\frac{9}{4}$ D、 $\frac{9}{2}$

查看试题解析
6. 如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB＝30°，⊙O的半径为5 cm，则圆心O到弦CD的距离是（）

A、 $\frac{5}{2}$ cm B、3 cm C、3 $\sqrt{3}$ cm D、6 cm

查看试题解析
7. 如图，五边形 $A B C D E$ 是 $⊙ O$ 的内接正五边形， $A F$ 是 $⊙ O$ 的直径，则 $∠ B D F$ 的度数是（）

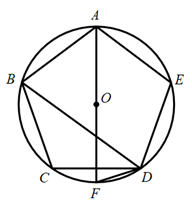A、18° B、36° C、 $54 °$ D、72°

查看试题解析
8. 如图在△ABC中，D、E分别是边AB、BC上的点，且DE $∥$ AC ，若S_△BDE：S_△CDE=2：3，则S_△DOE：S_△AOC的值为（）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{4}{9}$ D、 $\frac{4}{25}$

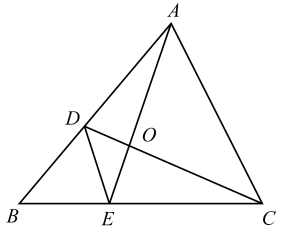查看试题解析
9. 如图，王虎使一长为4cm，宽为3cm的长方形木板，在桌面上做无滑动的翻滚（顺时针方向）木板上点A位置变化为A→A₁→A₂ ，其中第二次翻滚被桌面上一小木块挡住，使木板与桌面成30°角，则点A翻滚到A₂位置时共走过的路径长为（）

A、10cm B、 $4 π$ cm C、 $\frac{7}{2} π$ cm D、 $\frac{5}{2} π$ cm

查看试题解析
10. 图，抛物线 $y = \frac{1}{2} x^{2} - \frac{1}{2} x - 3$ 的图像与x轴交于点A，B，交y轴于点C，动点P在射线AB运动，作△BCP的外接圆⊙M，当圆心M落在该抛物线上时，则AP的值（）

A、3 B、4 C、5 D、3.5

查看试题解析

二、填空题

11. 抛物线 $y = {(x - 3)}^{2} - 5$ 的顶点坐标是

查看试题解析
12. 半径为 $2$ ，圆心角为 $12 0^{∘}$ 的扇形的面积为（结果保留 $π$ ）.

查看试题解析
13. 如图，在△ABC中， $D$ 为 $A B$ 边上一点，DE∥BC交 $A C$ 于点 $E$ ，若 $\frac{A D}{D B} = \frac{3}{5}$ ， DE=6，则BC=

查看试题解析
14. 在创建全国文明城市活动中，某市园林部门为了扩大市区的绿化面积，进行了大量的树木移栽.如表记录的是在相同条件下移栽某种幼树的棵数和成活棵数：
移栽棵树
100
500
1000
5000
10000
成活棵树
89
458
910
4498
9000
请根据表中数据估计，现园林部门移栽5000棵这种幼树，大约能成活棵.

查看试题解析
15. 如图，AB是半圆O的直径，∠ABD＝35°，点C是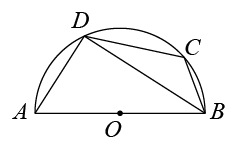 $\overset{⌢}{B D}$ 上的一点，则∠C= 度.

查看试题解析
16. 教练对小明推铅球的录像进行技术分析，发现铅球行进高度y（m）与水平距离x（m）之间的关系为 $y = - \frac{1}{12} {(x - 4)}^{2} + 3$ ，由此可知铅球推出的距离是m.

查看试题解析
17. 如图，在边长为7的正方形ABCD中放入四个小正方形后形成一个中心对称图形，其中两顶点E，F分别在边BC，AD上，则放入的四个小正方形的面积之和为 .

查看试题解析
18. 如图 1 是一款重型订书机，其结构示意图如图 2 所示.其主体部分为矩形 EFGH，由支撑杆 CD 垂直固定于底座 AB 上，且可以绕点 D 旋转.压杆 MN 与伸缩片 PG 连接，点 M 在HG 上，MN 可绕点 M 旋转，PG⊥HG ，DF＝8 cm，GF=2cm，不使用时，EF $∥$ AB，G 是 PF 中点，且点 D 在 NM 的延长线上，则 MG= cm，使用时如图3，按压 MN 使得 MN $∥$ AB，此时点 F 落在 AB 上，若 CD＝2 cm，则压杆 MN 到底座 AB 的距离为 cm

查看试题解析

三、解答题

19. 防疫期间，全市所有学校都严格落实测体温进校园的防控要求.某校开设了A、B、C三个测温通道，某天早晨，该校小明和小丽两位同学将随机通过测温通道进入校园.

(1)、小明从A测温通道通过的概率是；

(2)、利用画树状图或列表的方法，求小明和小丽从同一个测温通道通过的概率.

查看试题解析
20. 如图， $△ A B C$ 是格点三角形（三角形的三个顶点都在格点上），每个小正方形的边长均为1.

(1)、在图（1）中将 $△ A B C$ 绕点 $C$ 逆时针旋转 $90 °$ ，得到 $△ C D E$ .

(2)、在图（2）中找格 $P$ ，使以格点 $P$ 、 $C$ 、 $B$ 为顶点的三角形与 $△ A B C$ 相似，但不全等，请画出一个符合条件的三角形.

查看试题解析
21. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交于A、B点，与y轴交于C点，顶点为
D，其中点A、C的坐标分别是（－1，0）、（0，3）.

(1)、求抛物线的表达式与顶点D的坐标；

(2)、连结BD，过点O作OE⊥BD于点E，求OE的长.

查看试题解析
22. 如图 Rt△ABC中，∠ABC＝90°，P是斜边AC上一个动点，以BP为直径作⊙O交BC于点D，与AC的另一个交点E，且 $\overset{⌢}{D P} = \overset{⌢}{E P}$ 连接DE .

(1)、若 $\overset{⌢}{B D}$ ＝140°，求∠C的度数.

(2)、求证AB＝AP.

查看试题解析
23. 某景区商店销售一种成本价为 10 元/件的纪念品，已知这种纪念品的销售价不低于成本价，且物价部门规定销售价不得高于 24 元/件，经市场调查发现，该纪念品每天的销售量 y（件）与销售价 x（元/件）之间的函数关系如图所示.

(1)、求 y 关于 x 的函数解析式，并写出自变量 x 的取值范围；

(2)、求每天的销售利润 W（元）关于销售价 x（元/件）的函数解析式，并求出当每件的销售价为多少元时，每天的销售利润最大？最大利润为多少元？

查看试题解析
24. 如图，矩形ABCD中，BC=8，点F是AB边上一点（不与点B重合）△BCF的外接圆交对角线BD于点E，连接CF交BD于点G，连接EC.

(1)、求证：∠ECG=∠BDC.

(2)、当AB=6时，在点F的整个运动过程中，
①连接EF，若BF= $2 \sqrt{2}$ 时，求CE的长.
②当△CGE为等腰三角形时，求所有满足条件的CG的长.
直接写出荅案CG为 ▲

查看试题解析

移栽棵树	100	500	1000	5000	10000
成活棵树	89	458	910	4498	9000