浙江省台州市仙居县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-12-02 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形但不是轴对称图形的是 ( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,是必然事件的是 ( ).A、射击运动员射击一次,命中靶心 B、掷一次股子,向上一面的点数是6 C、经过有交通信号灯的路口,恰好遇到红灯 D、将油滴在水中,油浮在水上面3. 抛物线y=(x−2)2+3的顶点坐标是( )A、(2,3) B、(-2,3) C、(2,-3) D、(-2,-3)4. 用配方法解方程x2+1=8x,变形后的结果正确的是( )A、(x+4)2=15 B、(x+4)2=17 C、(x-4)2=15 D、(x-4)2=175. 用直角尺检查某圆弧形工件,根据下列检查的结果,能判断该工件一定是半圆的是( ).A、
2. 下列事件中,是必然事件的是 ( ).A、射击运动员射击一次,命中靶心 B、掷一次股子,向上一面的点数是6 C、经过有交通信号灯的路口,恰好遇到红灯 D、将油滴在水中,油浮在水上面3. 抛物线y=(x−2)2+3的顶点坐标是( )A、(2,3) B、(-2,3) C、(2,-3) D、(-2,-3)4. 用配方法解方程x2+1=8x,变形后的结果正确的是( )A、(x+4)2=15 B、(x+4)2=17 C、(x-4)2=15 D、(x-4)2=175. 用直角尺检查某圆弧形工件,根据下列检查的结果,能判断该工件一定是半圆的是( ).A、 B、
B、 C、
C、 D、
D、 6. 已知正六边形的边长为4,则这个正六边形外接圆的半径为( )A、2 B、2 C、4 D、47. 函数与函数(为常数,)在同一平面直角坐标系内的图象可能是 ( ).A、
6. 已知正六边形的边长为4,则这个正六边形外接圆的半径为( )A、2 B、2 C、4 D、47. 函数与函数(为常数,)在同一平面直角坐标系内的图象可能是 ( ).A、 B、
B、 C、
C、 D、
D、 8. 喜迎国庆佳节,天音百货某服装原价400元,连续两次降价a%后售价为225元。下列所列方程中,正确的是( )
8. 喜迎国庆佳节,天音百货某服装原价400元,连续两次降价a%后售价为225元。下列所列方程中,正确的是( )
A、400(1+a%)2=225 B、400(1-2a%)=225 C、400(1-a%)2=225 D、400(1-a2%)=2259. 已知二次函数 , 当 时, , 则当 时,的取值范围为 ( )A、 B、 C、 D、不能确定10. 对于平面上的点和一条线 , 点与线上各点的连线中,最短的线段的长度叫做点到线的距离,记为 , 以边长为6的正方形各边组成的折线为 , 若 , 则满足这样条件的所有点组成的图形 (实线图) 是 ( ).A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 抛物线与轴的交点坐标是.12. 如图是用计算机模拟抛掷一枚啤酒瓶盖试验的结果,由此可以推断,抛掷该啤酒瓶盖一次,“凸面向上”的概率是. (精确到 0.001).
 13. 如图,把一个半径为的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面 (衔接处无缝隙且不重叠),则圆锥底面半径是cm.
13. 如图,把一个半径为的圆形硬纸片等分成三个扇形,用其中一个扇形制作成一个圆锥形纸筒的侧面 (衔接处无缝隙且不重叠),则圆锥底面半径是cm. 14. 已知反比例函数 , 若 , 则的取值范围是.15. 如图,在一块长为22m,宽为14m的矩形空地内修建三条宽度相等的小路(阴影部分),其余部分种植花草.若花草的种植面积为240m2 , 则小路的宽为m.
14. 已知反比例函数 , 若 , 则的取值范围是.15. 如图,在一块长为22m,宽为14m的矩形空地内修建三条宽度相等的小路(阴影部分),其余部分种植花草.若花草的种植面积为240m2 , 则小路的宽为m. 16. 在Rt中, , 把绕点逆时针旋转得到 , 连接 , 当旋转角 为度时,.
16. 在Rt中, , 把绕点逆时针旋转得到 , 连接 , 当旋转角 为度时,.
三、解答题
-
17. 解方程:(1)、(2)、18. 小明和爸爸玩“石头”、“剪刀”、 “剪刀”的游戏,游戏规则:每局游戏每人用一只手可以出石头、 剪刀、布三种手势中的一种;石头赢剪刀,剪刀赢布,布赢石头;若两人出相同手势,则算平局.(1)、在一局游戏中,小明决定出“剪刀”,求他赢爸爸的概率;(2)、用列举法求一局游戏中两人出现平局的概率.19. 如图所示,是的一条弦, , 垂足为 , 交于点 , 点在上,.
 (1)、求的度数;(2)、若 , 求的长.20. 一条抛物线由抛物线平移得到,对称轴为直线 , 并且经过点.(1)、求该抛物线的解析式,并指出其顶点坐标;(2)、该抛物线由抛物线经过怎样平移得到?21. 如图,在边长为1的正方形网格中,线段绕某点顺时针旋转得到线段 , 点与点是对应点,点与点是对应点.
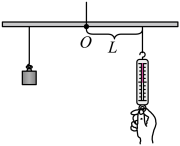
(1)、求的度数;(2)、若 , 求的长.20. 一条抛物线由抛物线平移得到,对称轴为直线 , 并且经过点.(1)、求该抛物线的解析式,并指出其顶点坐标;(2)、该抛物线由抛物线经过怎样平移得到?21. 如图,在边长为1的正方形网格中,线段绕某点顺时针旋转得到线段 , 点与点是对应点,点与点是对应点. (1)、在图中画出旋转中心(保留画图痕迹);(2)、求旋转过程中点经过的路径长.22. 如图,取一根长1米的质地均匀木杆,用细绳绑在木杆的中点处并将其吊起来,在中点的左侧距离中点处挂一个重牛的物体,在中点右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧称与中点的距离(单位:),看弹簧秤的示数(单位:牛,精确到牛) 有什么变化,小慧在做此 《数学活动》时,得到下表的数据:
(1)、在图中画出旋转中心(保留画图痕迹);(2)、求旋转过程中点经过的路径长.22. 如图,取一根长1米的质地均匀木杆,用细绳绑在木杆的中点处并将其吊起来,在中点的左侧距离中点处挂一个重牛的物体,在中点右侧用一个弹簧秤向下拉,使木杆保持平衡,改变弹簧称与中点的距离(单位:),看弹簧秤的示数(单位:牛,精确到牛) 有什么变化,小慧在做此 《数学活动》时,得到下表的数据:5
10
15
20
25
30
35
40
结果老师发现其中有一个数据明显有错误.
(1)、你认为当L=cm 时所对应的数据是明显错误的;(2)、在已学过的函数中选择合适的模型求出与的函数关系式;(3)、若弹簧秤的最大量程是60牛,求的取值范围.23. 如图,在中,弦与半径形成的夹角 , 点是优弧上的一动点,切线与射线相交于点. (1)、与满足的数量关系是.(2)、当时,求阴影部分的面积;(3)、当是多少度时,为等腰三角形?通过推理说明理由.24. 蔗糖是决定杨梅果实中糖度的主要成分,某果农种植东魁杨梅,5月26日检测到杨梅果实中的蔗糖含量为 , 从5月27日开始到6月1日,测量出蔗糖含量数据,并根据这些数据建立蔗糖含量变化率(蔗糖含量变化率=当天的蔗糖含量-上一天的蔗糖含量/上一天的蔗糖含量)与生长天数 表示5月26日)的函数关系是: . 根据这一函数模型解决下列问题:(1)、这种杨梅果实中蔗糖含量增长最快的是哪一天?请说明理由.(2)、求出这种杨梅果实中蔗糖含量在哪一天最高;(3)、当蔗糖含量最高时,杨梅口感最好,计划用6天时间采摘完这批杨梅,请给这位果农提出采摘日期的合理化建议.
(1)、与满足的数量关系是.(2)、当时,求阴影部分的面积;(3)、当是多少度时,为等腰三角形?通过推理说明理由.24. 蔗糖是决定杨梅果实中糖度的主要成分,某果农种植东魁杨梅,5月26日检测到杨梅果实中的蔗糖含量为 , 从5月27日开始到6月1日,测量出蔗糖含量数据,并根据这些数据建立蔗糖含量变化率(蔗糖含量变化率=当天的蔗糖含量-上一天的蔗糖含量/上一天的蔗糖含量)与生长天数 表示5月26日)的函数关系是: . 根据这一函数模型解决下列问题:(1)、这种杨梅果实中蔗糖含量增长最快的是哪一天?请说明理由.(2)、求出这种杨梅果实中蔗糖含量在哪一天最高;(3)、当蔗糖含量最高时,杨梅口感最好,计划用6天时间采摘完这批杨梅,请给这位果农提出采摘日期的合理化建议.