浙江省台州市温岭市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-12-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列4个数字中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知x＝1是方程x²﹣3x+c＝0的一个根，则实数c的值是（）

A、﹣1 B、0 C、1 D、2

查看试题解析
3. 下列成语或词语所反映的事件中，发生的可能性最小的是（）

A、瓜熟蒂落 B、守株待兔 C、旭日东升 D、瓮中捉鳖

查看试题解析
4. 反比例函数y= $\frac{- 3}{x}$ ，关于其函数图象下列说法错误的是（）

A、位于第二、四象限 B、图象过点（-1，3） C、关于原点成中心对称 D、y随x的增大而增大

查看试题解析
5. 2021年9月份，全国新冠疫苗当月接种量约为1.4亿剂次，11月份新冠疫苗当月接种量达到2.3亿剂次，若设平均每月的增长率为x，则下列方程中符合题意的是（）

A、1.4x² =2.3 B、1.4（1+x²）=2.3 C、1.4（1+x）² =2.3 D、1.4（1+2x）=2.3

查看试题解析
6. 将一个圆心角为120°，半径为6的扇形围成一个圆锥的侧面，则该圆锥底面圆的半径为（）

A、2 B、6 C、6 $\sqrt{3}$ D、18

查看试题解析
7. 如图，是三个反比例函数y₁= $\frac{k_{1}}{x}$ ， y₂= $\frac{k_{2}}{x}$ ， y₃= $\frac{k_{3}}{x}$ 在x轴上方的图象，则k₁、k₂、k₃的大小关系为（）

A、k₁> k₂>k₃ B、k₂> k₁> k₃ C、k₃> k₂> k₁ D、k₃> k₁> k₂

查看试题解析
8. 如图，等腰直角三角形ABC中，∠A=90°，BC=8，点D、点E分别是BC、AC边上的点，DE//AB则S_△BDE的最大值是（）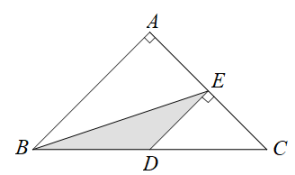

A、3 B、4 C、5 D、6

查看试题解析
9. 如图，⊙O是△ABC的外接圆，将△ABC绕点C顺时针旋转至△EDC，使点E在⊙O上，再将△EDC沿CD翻折，点E恰好与点A重合，已知∠BAC=36°，则∠DCE的度数是（）

A、24 B、27 C、30 D、33

查看试题解析
10. 如图，放置含30°的直角三角板，使点B在y轴上，点C在双曲线y= $\frac{k}{x}$ 上，且AB⊥y轴，BC的延长线交x轴于点D，若S_△ACD=3.则k=（）

A、3 B、3 $\sqrt{3}$ C、6 D、9

查看试题解析

二、填空题

11. 抛物线 $y = - 2 (x - 3)^{2} + 5$ 的顶点坐标为.

查看试题解析

12. 植树节过后，历下区园林绿化管理局为了考察树苗的成活率，于是进行了现场统计，表中记录了树苗的成活情况，则由此估计这种树苗成活的概率约为（结果精确到0.1）

植树总数 $n$	400	1500	3500	7000	9000	14000
成活数 $m$	369	1335	3203	6335	8073	12628
成活的频率 $\frac{m}{n}$	0.923	0.890	0.915	0.905	0.897	0.902

查看试题解析

13. 如图，菱形ABCD， $∠ A = 60 °$ ， $A B = 3$ ，分别以A，B，C，D为圆心，边长为半径画弧，得到一个眼状图形，则阴影部分的面积为（结果保留 $π$ ）.

查看试题解析
14. 把一个球放入长方体纸盒，球的一部分露出盒外，球与纸盒内壁都刚好相切，其截面如图所示，若露出部分的高度为6cm，AF=DE=3cm，则这个球的半径是cm.

查看试题解析
15. 把抛物线y=x²-2x-c（c>0）在直线y=c上方部分沿直线y=c对折，若对折后的部分在x轴上截得的线段长是6个单位，则c=.

查看试题解析
16. 如图是三个正方形组成的图案，实线围成的三个封闭部分面积分别为S₁ ， S₂ ， S₃ ，若S₁=1，则S₂= ， S₃=.

查看试题解析

三、解答题

17. 解方程：x²﹣6x+5=0．

查看试题解析
18. 如图所示，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（0，3），B（-1，0），C（3，-1）（每个方格的边长均为1个单位长度）.

(1)、将△ABC绕点A逆时针旋转90°，画出旋转后得到的△AB₁C₁

(2)、直接写出在旋转过程中，点C经过的格点坐标（C，C₁除外，格点指小正方形的顶点）.

查看试题解析
19. 全面两孩政策实施后，甲、乙两个家庭有了各自的规划，假定生男生女的概率相同，回答下列问题：

(1)、甲家庭已有一个男孩，准备再生一个孩子，则第二个孩子是女孩的概率是；

(2)、乙家庭没有孩子，准备生两个孩子，求至少有一个孩子是女孩的概率．

查看试题解析
20. 如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD.

(1)、求证：CD是⊙O的切线；

(2)、若AC=8，CD=12，求半径的长度.

查看试题解析
21. 如图，一次函数y₁=k₁x+b（x>0）的图象与反比例函数y₂= $\frac{k_{2}}{x}$ （x>0）的图象交于点A（m，6）、点B（3，2）.

(1)、求一次函数与反比例函数的解析式；

(2)、根据图象直接写出：当x为时，kx+b- $\frac{k_{2}}{x}$ <0.

查看试题解析
22. 在△ABC中，AB=AC，点D为平面内一点.

(1)、观察猜想：如图1，当∠BAC=90°，点D在BC上时，探究BD²、DC²与AD²之间的数量关系，我们可以把△ABD绕着点A逆时针旋转90°得△ACE，根据图形，请你通过探究直接写出BD²、DC²与AD²之间的数量关系：；

(2)、类比探究：如图2，当∠BAC=60°时，点D为△ABC外一点，将△ABD顺时针旋转后得到△BCE若D、E、C三点在一直线上，求∠ADB的度数；

(3)、拓展应用：如图3，已知∠BAC=∠BDA=120°，DC=10，AD=2 $\sqrt{3}$ ，求BD的长.

查看试题解析
23. 如图，⊙O是△ABC的外接圆，AB为直径，CD平分∠ACB交⊙O于点D，OE⊥AC交AC于点E，交CD于点F，连接BD；

(1)、如图1，求∠OFD的度数.

(2)、如图2，过O作OG⊥CD于G，交BC于H，求证：BH=OF；

(3)、如图3，连接BF，若BF=BD，OF=1，求⊙O半径.（画出辅助线，写出简要过程）

查看试题解析
24. 疫情就是命令，台州新冠疫情防控指挥部安排某中学进行了核酸检测采样演练，演练下午3点开始，设6个采样窗口，每个窗口采样速度相同，学生陆续到操场排队，4点半排队完毕，小明就排队采样的时间和人数进行了统计，得到下表：
时间x（分）
0
15
30
45
75
90
95
100
110
人数y（个）
60
115
160
195
235
240
180
120
0
小明把记录的数据，在平面直角坐标系里，描成点连成线，发现满足学过的某些函数图象如图，请你解答：

(1)、求曲线ABC部分的函数解析式；

(2)、若排队人数在220人及以上，即为满负荷状态，问满负荷状态的时间持续多长？

(3)、如果采样进行45分钟后，为了减少扎堆排队的时间，指挥部要求4点15分后，采样可以随到随采，那么至少需新增多少个采样窗口？

(4)、疫情防控指挥部按照每个采样窗口与某中学相同采样速度对员工人数为600的某单位进行全员核酸检测，如果采样时间t（分钟）控制在30分钟到60分钟之间（即30≤t≤60），则开设的采样窗口数量n（个）的范围是 .

查看试题解析

时间x（分）	0	15	30	45	75	90	95	100	110
人数y（个）	60	115	160	195	235	240	180	120	0