（人教版）2022-2023学年度第一学期七年级数学有理数的乘除法期末复习

试卷更新日期：2022-12-01 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列说法：
①若一个数的倒数等于它本身，则这个数是1或-1；②|a|= |-2|，则a=-2；

③2³x²y+x+1是六次三项式；④若a，b互为相反数，则a+b=0．

其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 2022的倒数是（）

A、-2022 B、2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
3. 观察下列图形，则第2022个图形中三角形的个数是（）

A、8084 B、8088 C、2021 D、2022

查看试题解析
4. 下列运算错误的是（）

A、（-2）×（-3） ×5＝ 30 B、（- $\frac{1}{2}$ ）×（-6）×0＝3 C、（-5）×（-2）×（-4）＝ -40 D、（-3）×（-2）×（-4）＝ -24

查看试题解析
5. 如果 $ab > 0$ ， $a + b < 0$ ，则这 $a$ ， $b$ 的符号为（）

A、同正 B、同负 C、一正一负 D、无法确定

查看试题解析
6. 按如图所示的运算程序，若输入m的值是-2，则输出的结果是（）

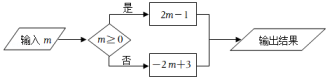A、-1 B、3 C、-5 D、7

查看试题解析
7. 将2019减去它的 $\frac{1}{2}$ ，再减去余下的 $\frac{1}{3}$ ，再减去余下的 $\frac{1}{4}$ ，最后减去余下的 $\frac{1}{2019}$ ，则最后的差是（）

A、 $\frac{1}{2019}$ B、 $\frac{2018}{2019}$ C、 ${(\frac{2018}{2019})}^{2}$ D、1

查看试题解析
8. 若 $| m - 3 | + (n + 2)^{2} = 0$ ，则 $m + 2 n$ 的值为（）

A、-4 B、-1 C、0 D、4

查看试题解析
9. 计算 $12 - 7 \times (- 4) + 8 \div (- 2)$ 的结果是

A、-24 B、-20 C、6 D、36

查看试题解析
10. 一组数据：2，1，3，x，7， $- 9$ ， …，满足“从第三个数起，若前两个数依次为a、b，则紧随其后的数就是 $2 a - b$ ”，例如这组数中的第三个数“3”是由“ $2 \times 2 - 1$ ”得到，那么该组数据中的x为（）．

A、 $- 1$ B、 $- 2$ C、1 D、2

查看试题解析

二、填空题

11. 若 $a 、 b$ 互为相反数， $c 、 d$ 互为倒数，则 $\frac{1}{c d} - a - b =$ .

查看试题解析
12. 一座两道环路的数字迷宫如图所示，外环两个路口的数字分别为－5，4，内环两个路口的数字分别为－3，2．要想进入迷宫中心需破解密码：两个路口的数相乘，若乘积最大，沿这两个路口就可到达迷宫中心，则乘积最大的值是．

查看试题解析
13. 在2，5，-3，-5这四个数中任意取两个数相除，所得的商最小为.

查看试题解析
14. “24点游戏”指的是将一副扑克牌中任意抽出四张，根据牌面上的数字进行加减乘除混合运算（每张牌只能使用一次），使得运算结果是24或者是﹣24，现抽出的牌所对的数字是4，﹣5，3，﹣1，请你写出刚好凑成24的算式．

查看试题解析
15. 有这样一个数字游戏，用 $1$ ， $- 5$ ， $11$ ， $a$ 四个数通过加、减、乘、除四则运算，可以得到结果 $24$ ．若 $a$ 是绝对值不大于 $5$ 的整数，请写出一个满足条件的算式：．

查看试题解析

三、解答题

16. 已知a，b互为相反数，且a≠0，c，d互为倒数，m的绝对值是最小的正整数，
求m²- $\frac{a}{b} + \frac{2021 (a + b)}{2022}$ -cd的值．

查看试题解析
17. 已知a、b互为相反数 $(a \neq 0)$ ， c、d互为倒数，x的绝对值等于2，试求 $x - \frac{3 a}{b} + (a + b)^{2021} - (- c d)^{2022}$ 的值．

查看试题解析
18. 请你仔细阅读下列材料：计算：
$(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5})$

解法 $1$ ：按常规方法计算

原式 $= (- \frac{1}{30}) \div [\frac{2}{3} + \frac{1}{6} - (\frac{1}{10} + \frac{2}{5})] = (- \frac{1}{30}) \div (\frac{5}{6} - \frac{1}{2}) = (- \frac{1}{30}) \times 3 = - \frac{1}{10}$

解法 $2$ ：简便计算，先求其倒数

原式的倒数为： $(\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \div (- \frac{1}{30}) = (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) \times (- 30) = - 20 + 3 - 5 + 12 = - 10$

故 $(- \frac{1}{30}) \div (\frac{2}{3} - \frac{1}{10} + \frac{1}{6} - \frac{2}{5}) = - \frac{1}{10}$

再根据你对所提供材料的理解，模仿以上两种方法分别进行计算： $(- \frac{1}{56}) \div (\frac{3}{8} - \frac{3}{14} + \frac{1}{2} - \frac{2}{7})$

查看试题解析

四、综合题

19. 已知：数a，b，c在数轴上的对应点如图所示，

(1)、在数轴上表示－a；

(2)、比较大小（填“〈”或“〉”或“＝”）：a+b0，－3c0，c-a0；

(3)、化简 $| a + b | - | - 3 c | + | c - a |$

查看试题解析
20. 已知非零有理数a，b，c满足 $a b > 0$ ， $b c > 0$ .

(1)、求 $\frac{| a b |}{a b} + \frac{a c}{| a c |} + \frac{| b c |}{b c}$ 的值；

(2)、若 $a + b + c < 0$ ，求 $\frac{| a |}{a} + \frac{b}{| b |} + \frac{| c |}{c} + \frac{| a b c |}{a b c}$ 的值.

查看试题解析
21. 学习了有理数的乘法之后，老师出了两道例题，下面是小方的计算过程，请认真阅读并完成相应任务：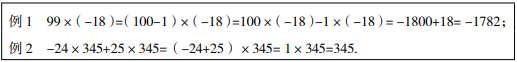

(1)、任务一：例1，例2都用到的运算律是；

(2)、任务二：请你参照上述例1，例2，用运算律简便计算：
① $999 \times (- 26)$ ；

② $999 \times 124 \frac{5}{7} - 999 \times 24 \frac{4}{7} + 333 \times (- \frac{3}{7})$ ．

查看试题解析
22. 一只蚂蚁从某点A出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程（单位：厘米）依次为：+2，-3，+12，-8，-7，+16，-12，

(1)、通过计算说明蚂蚁是否回到起点A；

(2)、如果蚂蚁爬行的速度为0.5厘米/秒，那么蚂蚁共爬行了多长时间．

查看试题解析
23. 有个写运算符号的游戏：在“3□（2□3） □ $\frac{4}{3}$ □4” 中的每个 □ 内，
填入+，-，×，÷中的某一个（可重复使用），然后计算结果．

(1)、请计算琪琪填入符号后得到的算式： $3 \times （ 2 \div 3 ） - \frac{4}{3} \div 4$ ；

(2)、嘉嘉填入符号后得到的算式是 $3 \div （ 2 \times 3 ） \times \frac{4}{3} □ 4$ ，一不小心擦掉了□里的运算符号，但她知道结果是 $- \frac{10}{3}$ ，请推算□内的符号．（请写出计算过程）

查看试题解析

（人教版）2022-2023学年度第一学期七年级数学 有理数的乘除法 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）2022-2023学年度第一学期七年级数学有理数的乘除法期末复习