上海市嘉定区2022-2023学年九年级上学期数学期中考试卷
试卷更新日期:2022-12-01 类型:期中考试
一、单选题
-
1. 如果 , 那么下列各式不一定成立的是( )A、 B、 C、 D、2. 已知线段a、b、c,作线段x,使 , 下列每个图的两条虚线都是平行线,则正确的作法是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列命题正确的是( )A、如果||=||,那么= B、如果、都是单位向量,那么= C、如果=k(k≠0),那么∥ D、如果m=0或= , 那么m=04. 下列命题中,属于真命题的是( )A、两个菱形一定相似 B、两个等腰直角三角形一定相似 C、两个矩形一定相似 D、两个周长相等的三角形一定相似5. 在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )A、DEBC B、∠AED=∠B C、 D、6. 如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若AB= , 则此三角形移动的距离是( )
3. 下列命题正确的是( )A、如果||=||,那么= B、如果、都是单位向量,那么= C、如果=k(k≠0),那么∥ D、如果m=0或= , 那么m=04. 下列命题中,属于真命题的是( )A、两个菱形一定相似 B、两个等腰直角三角形一定相似 C、两个矩形一定相似 D、两个周长相等的三角形一定相似5. 在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )A、DEBC B、∠AED=∠B C、 D、6. 如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若AB= , 则此三角形移动的距离是( ) A、-1 B、 C、1 D、
A、-1 B、 C、1 D、二、填空题
-
7. 已知线段a=2厘米,c=8厘米,则线段a和c的比例中项b是厘米.8. 已知线段AB=4,点P是线段AB的黄金分割点,则AP的长为 .9. 计算:= .10. 在的地图上,某城市A与另一个城市B的距离是2.4cm,那么城市A与B的实际距离为千米.11. 如图,已知D是△ABC的边AC上一点,且AD=2DC . 如果 , ,那么向量 关于 、 的分解式是 .
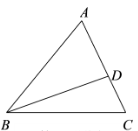 12. 如图,已知 , , 那么 .
12. 如图,已知 , , 那么 . 13. 如图,已知在平行四边形中,点E在边上,射线交的延长线于点F, , , 那么的长为 .
13. 如图,已知在平行四边形中,点E在边上,射线交的延长线于点F, , , 那么的长为 . 14. 直角三角形的两直角边长分别为3和4,则重心与斜边中点的距离是 .15. 如图,已知在中,边 , 高 , 正方形的顶点E、F在边上,顶点H、G分别在边和上,那么这个正方形的边长等于 .
14. 直角三角形的两直角边长分别为3和4,则重心与斜边中点的距离是 .15. 如图,已知在中,边 , 高 , 正方形的顶点E、F在边上,顶点H、G分别在边和上,那么这个正方形的边长等于 . 16. 如图,已知 , , , 则= .
16. 如图,已知 , , , 则= . 17. 如图,四边形都是正方形, °
17. 如图,四边形都是正方形, ° 18. 如图,中, , , 是边上的中线,将绕着点A旋转,点B与点C的对应点分别是点E、F,如果点E恰好在的延长线上,那么的长是 .
18. 如图,中, , , 是边上的中线,将绕着点A旋转,点B与点C的对应点分别是点E、F,如果点E恰好在的延长线上,那么的长是 .
三、解答题
-
19. 已知: , 且 , 求的值.20. 已知,如图,在中,D是的中点,重心G在上.
 (1)、如果向量 , , 请用、表示向量;(2)、在原图中过点D画的平行线交于点E,并画出在、方向上的分向量.(不要求写作法,要写出结论)21. 《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上).
(1)、如果向量 , , 请用、表示向量;(2)、在原图中过点D画的平行线交于点E,并画出在、方向上的分向量.(不要求写作法,要写出结论)21. 《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上). 22. 如图,已知 , 与相交于点E,点F在线段上, , .
22. 如图,已知 , 与相交于点E,点F在线段上, , . (1)、求证:;(2)、求 .23. 已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC交于点F.
(1)、求证:;(2)、求 .23. 已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC交于点F. (1)、求证:△ABD∽△FDC;(2)、求证:AE2=BE•EF.
(1)、求证:△ABD∽△FDC;(2)、求证:AE2=BE•EF.



