上海市奉贤区七校联考2022-2023学年九年级上学期期中考试数学试卷
试卷更新日期:2022-12-01 类型:期中考试
一、单选题
-
1. 下列说法正确的是( )A、有一个角等于100°的两个等腰三角形相似 B、两个矩形一定相似 C、有一个角等于45°的两个等腰三角形相似 D、相似三角形一定不是全等三角形2. 如图,小正方形的边长为均为1,下列各图(图中小正方形的边长均为1)阴影部分所示的三角形中,与相似的三角形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 已知Rt△ABC中,∠C=90°,AC=4,BC=6,那么下列各式中,正确的是( )A、 B、 C、 D、4. 在中,点D、E在边、上, , 要使 , 可添加下列条件中的( )A、 B、 C、 D、5. 在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )A、DEBC B、∠AED=∠B C、 D、6. 已知:线段a,b,c,求作线段x,使x= , 以下作法正确的是( )A、
3. 已知Rt△ABC中,∠C=90°,AC=4,BC=6,那么下列各式中,正确的是( )A、 B、 C、 D、4. 在中,点D、E在边、上, , 要使 , 可添加下列条件中的( )A、 B、 C、 D、5. 在△ABC中,点D、E分别在边AB、AC上,联结DE,那么下列条件中不能判断△ADE和△ABC相似的是( )A、DEBC B、∠AED=∠B C、 D、6. 已知:线段a,b,c,求作线段x,使x= , 以下作法正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
7. 线段b是线段a和线段c的比例中项,若a=1cm, b =3cm,则c= cm.8. 若 , 则的值为 .9. 在比例尺是的交通游览图上,某隧道长约 , 那么它的实际长度约为m.10. 在以O为坐标原点的直角坐标平面内有一点A(4,2),如果AO与x轴正半轴的夹角为α,那么cosα= .11. 已知线段NN=6,点O是线段MN的黄金分割点,且MO>NO,那么MO的长为 .12. 如图,在平行四边形ABCD中, , , 的平分线交BC于点E,交DC的延长线于点F,于点G,若 , 则的周长为 .
 13. 如图,点G是的重心,连接并延长交于点D,交于点E,若 , 那么 .
13. 如图,点G是的重心,连接并延长交于点D,交于点E,若 , 那么 . 14. 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为1,则平行四边形ABCD的面积为 .
14. 如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为1,则平行四边形ABCD的面积为 . 15. 如图,已知点D为中边的中点, , 直线交于点G,交的延长线于点F,若 , , 则的长为 .
15. 如图,已知点D为中边的中点, , 直线交于点G,交的延长线于点F,若 , , 则的长为 . 16. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米.
16. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米. 17. 我们知道,互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果坐标系中两条坐标轴不垂直,那么这样的坐标系称为“斜坐标系”.如图1,P是斜坐标系中的任意一点,与直角坐标系相类似,过点P分别作两坐标轴的平行线,与x轴、y轴交于点M、N,若M、N在x轴、y轴上分别对应实数a、b,则有序实数对叫做点P在斜坐标系中的坐标.如图2,在斜坐标系中,已知点、点是线段上的任意一点,试求x、y之间一定满足的一个等量关系式: .
17. 我们知道,互相垂直且有公共原点的两条数轴构成平面直角坐标系.如果坐标系中两条坐标轴不垂直,那么这样的坐标系称为“斜坐标系”.如图1,P是斜坐标系中的任意一点,与直角坐标系相类似,过点P分别作两坐标轴的平行线,与x轴、y轴交于点M、N,若M、N在x轴、y轴上分别对应实数a、b,则有序实数对叫做点P在斜坐标系中的坐标.如图2,在斜坐标系中,已知点、点是线段上的任意一点,试求x、y之间一定满足的一个等量关系式: . 18. 如图,在矩形中,已知 , 如果将矩形沿直线l翻折后,点A落在边的中点E处,直线l分别与边交于点M、N,如果 , 那么的长为 .
18. 如图,在矩形中,已知 , 如果将矩形沿直线l翻折后,点A落在边的中点E处,直线l分别与边交于点M、N,如果 , 那么的长为 .
三、解答题
-
19. 已知 , 且 , 求代数式的值.20. 如图,已知直线 , 直线和被、、所截.若 , , .
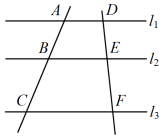 (1)、求、的长;(2)、如果 , , 求的长.21. 如图,已知在四边形中, , , , .
(1)、求、的长;(2)、如果 , , 求的长.21. 如图,已知在四边形中, , , , . (1)、的长;(2)、如果点E为的中点,连接 , 求的正切值.22. 如图,在中,点D在边上,点F、E在边上,且 ,
(1)、的长;(2)、如果点E为的中点,连接 , 求的正切值.22. 如图,在中,点D在边上,点F、E在边上,且 , (1)、求证:;(2)、如图求的值.23. 如图,已知菱形ABCD,点E是AB的中点,AF⊥BC于点F,联结EF、ED、DF,DE交AF于点G,且AE2=EG•ED.
(1)、求证:;(2)、如图求的值.23. 如图,已知菱形ABCD,点E是AB的中点,AF⊥BC于点F,联结EF、ED、DF,DE交AF于点G,且AE2=EG•ED.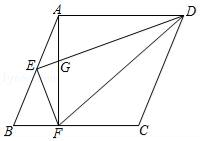 (1)、求证:DE⊥EF;(2)、求证:BC2=2DF•BF.24. 已知在平面直角坐标系中,直线:与x轴交于点A,将l向下平移16个单位后交y轴于点B.
(1)、求证:DE⊥EF;(2)、求证:BC2=2DF•BF.24. 已知在平面直角坐标系中,直线:与x轴交于点A,将l向下平移16个单位后交y轴于点B. (1)、求的余切值;(2)、点C在平移后的直线上,其纵坐标为 , 联结 , 其中与y轴交于点E,求的值;(3)、点M在直线上且位于第一象限,联结 , 当时,求点M的坐标.25. 如图,在△ABC中,AB=10,BC=34,cos∠ABC= , 射线CM∥AB,D为线段BC上的一动点且和B,C不重合,联结DA,过点D作DE⊥DA交射线CM于点E,联结AE,作EF=EC,交BC的延长线于点F,设BD=x.
(1)、求的余切值;(2)、点C在平移后的直线上,其纵坐标为 , 联结 , 其中与y轴交于点E,求的值;(3)、点M在直线上且位于第一象限,联结 , 当时,求点M的坐标.25. 如图,在△ABC中,AB=10,BC=34,cos∠ABC= , 射线CM∥AB,D为线段BC上的一动点且和B,C不重合,联结DA,过点D作DE⊥DA交射线CM于点E,联结AE,作EF=EC,交BC的延长线于点F,设BD=x. (1)、如图1,当AD∥EF,求BD的长;(2)、若CE=y,求y关于x 的函数解析式,并写出定义域;(3)、如图2,点G在线段AE上,作∠AGD=∠F,若△DGE与△CDE相似,求BD的长.
(1)、如图1,当AD∥EF,求BD的长;(2)、若CE=y,求y关于x 的函数解析式,并写出定义域;(3)、如图2,点G在线段AE上,作∠AGD=∠F,若△DGE与△CDE相似,求BD的长.