山西省忻州市五台县2022-2023学年九年级上学期期中考试数学试卷
试卷更新日期:2022-12-01 类型:期中考试
一、单选题
-
1. 2022年第19届亚运会在杭州举行,吉祥物为智能小伙伴“江南忆”组合,其中吉祥物“宸宸”深受网民喜爱,结合你所学知识,从下列四个选项中选出能够和“宸宸”(如图)的图片成中心对称的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 已知一元二次方程 , 下列判断正确的是( )A、该方程有两个不相等的实数根 B、该方程有两个相等的实数根 C、该方程无实数根 D、该方程根的情况无法确定3. 对于抛物线 , 下列判断正确的是( )A、顶点 B、抛物线向左平移个单位长度后得到 C、抛物线与y轴的交点是 D、当时,y随x的增大而增大4. 如图所示,在中, , , 则的度数是( )
2. 已知一元二次方程 , 下列判断正确的是( )A、该方程有两个不相等的实数根 B、该方程有两个相等的实数根 C、该方程无实数根 D、该方程根的情况无法确定3. 对于抛物线 , 下列判断正确的是( )A、顶点 B、抛物线向左平移个单位长度后得到 C、抛物线与y轴的交点是 D、当时,y随x的增大而增大4. 如图所示,在中, , , 则的度数是( ) A、55° B、110° C、125° D、150°5. 将一个容积为600cm3的长方体包装盒剪开、铺平,纸样如图所示,根据题意,列出关于x的方程为( )
A、55° B、110° C、125° D、150°5. 将一个容积为600cm3的长方体包装盒剪开、铺平,纸样如图所示,根据题意,列出关于x的方程为( ) A、 B、 C、 D、6. 下表中列出的是一个二次函致的自变量x与函数y的几组对应值:下列各选项中,正确的是( )
A、 B、 C、 D、6. 下表中列出的是一个二次函致的自变量x与函数y的几组对应值:下列各选项中,正确的是( )x
…
0
1
3
…
y
…
4
6
4
…
A、函数的图象开口向上 B、函数的图象与x轴无交点 C、函数的最大值大于6 D、当时,对应函数y的取值范围是7. 筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且 被水面截得的弦 长为6米, 半径长为4米.若点C为运行轨道的最低点,则点C到弦 所在直线的距离是( )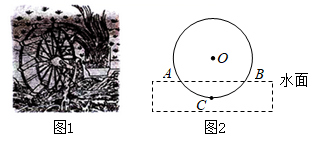 A、1米 B、 米 C、2米 D、 米8. 如图,在中, , 在平面内将绕点C旋转到位置,若 , 则的度数是( )
A、1米 B、 米 C、2米 D、 米8. 如图,在中, , 在平面内将绕点C旋转到位置,若 , 则的度数是( ) A、10° B、12° C、14° D、16°9. 如图,已知等腰 , , 以为直径的圆交于点D,过点D的的切线交于点E,若 , 则的半径是( )
A、10° B、12° C、14° D、16°9. 如图,已知等腰 , , 以为直径的圆交于点D,过点D的的切线交于点E,若 , 则的半径是( )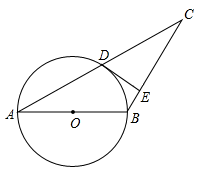 A、 B、5 C、6 D、10. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为( )A、 B、 C、 或 D、 或
A、 B、5 C、6 D、10. 已知 的直径 , 是 的弦, ,垂足为 ,且 ,则 的长为( )A、 B、 C、 或 D、 或二、填空题
-
11. 已知一个二次函数的图象开口向上,顶点坐标为 , 那么这个二次函数的解析式可以是 . (只需写一个).12. 将方程用配方法化为 , 则的值是 .13. ⊙O的半径为5cm,点O到直线AB的距离为d,当d=时,AB与⊙O相切.14.
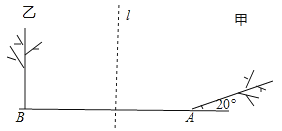
如图,请说出甲树是怎样由乙树变换得到的: .
 15. 如图,观察图中的尺规作图痕迹,若∠FMO=50°,则∠FOE的度数为 .
15. 如图,观察图中的尺规作图痕迹,若∠FMO=50°,则∠FOE的度数为 .
三、解答题
-
16. 关于 的一元二次方程 .
(1)、当 时,利用根的判别式判断方程根的情况;
(2)、若方程有两个相等的实数根,写出一组满足条件的 , 的值,并求此时方程的根.
17. 如图,是的直径,点P是上一点,且点P是弦的中点. (1)、依题意画出弦;(尺规作图不写作法,保留作图痕迹)(2)、若 , , 求的半径.18. ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
(1)、依题意画出弦;(尺规作图不写作法,保留作图痕迹)(2)、若 , , 求的半径.18. ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图: (1)、画出△ABC关于原点O的中心对称图形△A1B1C1 .(2)、将△ABC绕点A逆时针旋转90°得到△A2B2C2 , 则B2的坐标为 .(3)、求△A2B2C2面积.19. 已知,如图,AB是⊙O的直径,AD平分∠BAC交⊙O于点D,过点D的切线交AC的延长线于E.求证:DE⊥AE.
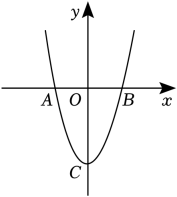
(1)、画出△ABC关于原点O的中心对称图形△A1B1C1 .(2)、将△ABC绕点A逆时针旋转90°得到△A2B2C2 , 则B2的坐标为 .(3)、求△A2B2C2面积.19. 已知,如图,AB是⊙O的直径,AD平分∠BAC交⊙O于点D,过点D的切线交AC的延长线于E.求证:DE⊥AE. 20. 如图,抛物线的顶点为C(1,4),交x轴于点A,B ( -1,0 ) 两点,交y轴于点D.
20. 如图,抛物线的顶点为C(1,4),交x轴于点A,B ( -1,0 ) 两点,交y轴于点D.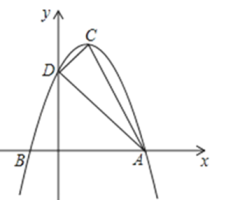 (1)、求抛物线的解析式,并直接写出点D的坐标,(2)、判断△ACD的形状,并求出△ACD的面积.21. 数学探究课上老师出了这样一道题:“如图,等边中有一点P,且 , , , 试求的度数.”小明和小军探讨时发现了一种求度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断.
(1)、求抛物线的解析式,并直接写出点D的坐标,(2)、判断△ACD的形状,并求出△ACD的面积.21. 数学探究课上老师出了这样一道题:“如图,等边中有一点P,且 , , , 试求的度数.”小明和小军探讨时发现了一种求度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断. (1)、在图中画出绕点A顺时旋转60°后的 , 并判断的形状是;(2)、试判断的形状,并说明理由;(3)、由(1)、(2)两问可知: .
(1)、在图中画出绕点A顺时旋转60°后的 , 并判断的形状是;(2)、试判断的形状,并说明理由;(3)、由(1)、(2)两问可知: .