吉林省长春市榆树市2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-01 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 下列二次根式中,与是同类二次根式的是( )A、 B、 C、 D、33. 若 , 则的值为( )A、 B、 C、 D、34. 下列计算正确的是( )A、 B、 C、 D、5. 用配方法解方程 , 下列变形正确的是( )A、 B、 C、 D、6. 如图, , 与相交于点G.若则的长为( )
 A、 B、 C、12 D、207. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )
A、 B、 C、12 D、207. 如图▱ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )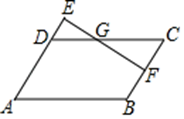 A、2:3 B、3:2 C、9:4 D、4:98. 某学校生物兴趣小组在该校空地上围了一块面积为的矩形试验田,用来种植蔬菜.如图,试验田一面靠墙,墙长 , 另外三面用长的篱笆围成,其中一边开有一扇宽的铁制小门.设试验田垂直于墙的一边的长为 , 则下列所列方程正确的是( )
A、2:3 B、3:2 C、9:4 D、4:98. 某学校生物兴趣小组在该校空地上围了一块面积为的矩形试验田,用来种植蔬菜.如图,试验田一面靠墙,墙长 , 另外三面用长的篱笆围成,其中一边开有一扇宽的铁制小门.设试验田垂直于墙的一边的长为 , 则下列所列方程正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. .10. 若 ,则x的取值范围是 .11. 一元二次方程根的判别式的值是 .12. 若x=1是关于x的一元二次方程x2+3mx+n=0的解,则6m+2n= .
13. 《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆 ,从木杆的顶端B观察井水水岸D , 视线 与井口的直径 交于点E , 如果测得 米, 米, 米,那么 为米.
 14. 如图,是等腰直角三角形, , D为边上一点,连接 , 过点B作 , 交的延长线于点E.若 , 则的值为 .
14. 如图,是等腰直角三角形, , D为边上一点,连接 , 过点B作 , 交的延长线于点E.若 , 则的值为 .
三、解答题
-
15. 计算: .16. 解方程:x2+5x+3=0.17. 如图①、图②均是的正方形网格,每个小正方形的顶点称为格点,的顶点均在格点上.只用无刻度的直尺,分别在图①、图②中,各画一个 , 使得与相似,且点P在格点上.
 18. 已知关于x的一元二次方程 .(1)、若方程的一个根为2,求m的值.(2)、求证:无论m取何实数,该方程总有两个不相等的实数根.19. 实数a、b在数轴上的位置如图所示.化简 .
18. 已知关于x的一元二次方程 .(1)、若方程的一个根为2,求m的值.(2)、求证:无论m取何实数,该方程总有两个不相等的实数根.19. 实数a、b在数轴上的位置如图所示.化简 .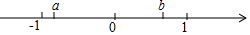 20. 如图, , 且 , 点D在内部,连接 .
20. 如图, , 且 , 点D在内部,连接 . (1)、求证: .(2)、若 , 且 , 求的长.21. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上.
(1)、求证: .(2)、若 , 且 , 求的长.21. 如图,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡在点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度DE=3.5m,点F到地面的高度CF=1.5m,灯泡到木板的水平距离AC=5.4m,墙到木板的水平距离为CD=4m.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上. (1)、求BC的长.(2)、求灯泡到地面的高度AG.22. 探究:如图①,直线l1∥l2∥l3 , 点C在l2上,以点C为直角顶点作∠ACB=90°,角的两边分别交l1与l3于点A、B,连结AB,过点C作CD⊥l1于点D,延长DC交l3于点E.
(1)、求BC的长.(2)、求灯泡到地面的高度AG.22. 探究:如图①,直线l1∥l2∥l3 , 点C在l2上,以点C为直角顶点作∠ACB=90°,角的两边分别交l1与l3于点A、B,连结AB,过点C作CD⊥l1于点D,延长DC交l3于点E. (1)、求证:△ACD∽△CBE.(2)、应用:如图②,在图①的基础上,设AB与l2的交点为F,若AC=BC,l1与l2之间的距离为2,l2与l3之间的距离为1,则AF的长度是 .23. 直播购物已经逐渐走进了人们的生活,某电商直播销售一款水杯,每个水杯的成本为30元.当每个水杯的售价为40元时,平均每月售出600个.通过市场调查发现,若售价每上涨1元,其月销售量就减少10个.(1)、当每个水杯的售价为45元时,平均每月售出个水杯,月销售利润是元.(2)、若每个水杯售价上涨x元 , 每月能售出个水杯(用含x的代数式表示).(3)、若月销售利润恰好为10000元,且尽可能让顾客得到实惠,求每个水杯的售价.24. 如图,已知直线与x轴交于点A,与y轴交于点B,动点C从点B出发,以每秒1个单位的速度沿方向匀速运动,同时动点D从点A出发,以每秒2个单位的速度沿方向向点O匀速运动,当一个点停止运动,另一个点也随之停止运动,设运动的时间为t秒().
(1)、求证:△ACD∽△CBE.(2)、应用:如图②,在图①的基础上,设AB与l2的交点为F,若AC=BC,l1与l2之间的距离为2,l2与l3之间的距离为1,则AF的长度是 .23. 直播购物已经逐渐走进了人们的生活,某电商直播销售一款水杯,每个水杯的成本为30元.当每个水杯的售价为40元时,平均每月售出600个.通过市场调查发现,若售价每上涨1元,其月销售量就减少10个.(1)、当每个水杯的售价为45元时,平均每月售出个水杯,月销售利润是元.(2)、若每个水杯售价上涨x元 , 每月能售出个水杯(用含x的代数式表示).(3)、若月销售利润恰好为10000元,且尽可能让顾客得到实惠,求每个水杯的售价.24. 如图,已知直线与x轴交于点A,与y轴交于点B,动点C从点B出发,以每秒1个单位的速度沿方向匀速运动,同时动点D从点A出发,以每秒2个单位的速度沿方向向点O匀速运动,当一个点停止运动,另一个点也随之停止运动,设运动的时间为t秒(). (1)、求的面积;(2)、用含有t的代数式表示C点的坐标;(3)、直接写出t为何值时,面积为;(4)、直接写出与相似时t的值.
(1)、求的面积;(2)、用含有t的代数式表示C点的坐标;(3)、直接写出t为何值时,面积为;(4)、直接写出与相似时t的值.