吉林省长春市农安县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{2} = 6$ C、 $\sqrt{8} \div \sqrt{2} = 4$ D、 $\sqrt{12} - \sqrt{3} = \sqrt{3}$

查看试题解析
2. 下列二次根式中，最简二次根式是（　　）

A、 $\sqrt{3 a^{2}}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{12}$ D、 $\sqrt{11 a}$

查看试题解析
3. 下列式子一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt{a + b^{2}}$ C、 $\sqrt{{(a - 1)}^{2}}$ D、 $\sqrt{a^{2} - 1}$

查看试题解析
4. 下列方程是关于x的一元二次方程的是（）

A、 $x + 2 y = 1$ B、 $x^{2} + x - 1 = x^{2}$ C、 $x^{2} + \frac{3}{x} = 8$ D、 $x^{2} - 5 x = 0$

查看试题解析
5. 将方程 $x^{2} - 6 x + 1 = 0$ 配方后，原方程可变形为（）

A、 $(x - 3)^{2} = 8$ B、 $(x - 3)^{2} = - 10$ C、 $(x + 3)^{2} = - 10$ D、 $(x + 3)^{2} = 8$

查看试题解析
6. 如图，学校课外生物小组试验园地的形状是长40米、宽34米的矩形，为便于管理，要在中间开辟一横两纵共三条等宽的小道，使种植面积为960平方米．则小道的宽为多少米？若设小道的宽为x米，则根据题意，列方程为（）

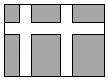A、 $(40 - 2 x) (34 - x) = 960$ B、 $40 \times 34 - 40 x - 34 x + 2 x^{2} = 960$ C、 $(40 - x) (34 - 2 x) = 960$ D、 $40 \times 34 - 40 x - 2 \times 34 x = 960$

查看试题解析
7. 已知3x=5y（y≠0），则下列比例式成立的是（）

A、 $\frac{x}{3} = \frac{5}{y}$ B、 $\frac{x}{5} = \frac{y}{3}$ C、 $\frac{x}{y} = \frac{3}{5}$ D、 $\frac{x}{3} = \frac{y}{5}$

查看试题解析
8. 如图，在 $△ A B C$ 中， $D E ∥ B C$ 交 $A B$ 于点D，交 $A C$ 于点E，下列式子不成立的是（）

A、 $\frac{A D}{D B} = \frac{A E}{E C}$ B、 $\frac{A B}{D B} = \frac{A C}{E C}$ C、 $\frac{A B}{A D} = \frac{A C}{A E}$ D、 $\frac{A D}{D B} = \frac{D E}{B C}$

查看试题解析
9. 如图，以点O为位似中心，将△ABC放大后得到 $△ A^{'} B^{'} C^{'}$ ，已知OB： $O B^{^{'}}$ ＝2：3，则△ABC与 $△ A^{'} B^{'} C^{'}$ 的面积之比为（　　）

A、1：3 B、1：9 C、2：3 D、4：9

查看试题解析
10. 如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC是相似三角形，则满足条件的点P的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 要使 $\sqrt{- a}$ 有意义，则a的取值范围是．

查看试题解析
12. 若 $\sqrt{28 n}$ 是整数，则正整数n的最小值为．

查看试题解析
13. 最简二次根式 $\sqrt{2 b + 1}$ 与 $\sqrt[a - 1]{7 - b}$ 是同类二次根式，则a＝， b＝．

查看试题解析
14. 若关于x的一元二次方程 $k x^{2} + 2 x - 1 = 0$ 有两个实数根，则k的取值范围是．

查看试题解析
15. 己如实数m是方程 $x^{2} - 4 x - 2 = 0$ 的一个根，则代数式 $2 m^{2} - 8 m$ 的值为．

查看试题解析
16. 对于任意不相等的两个实数a，b（a＞b）定义一种新运算a※b＝ $\frac{\sqrt{a + b}}{\sqrt{a - b}}$ ，如3※2＝ $\frac{\sqrt{3 + 2}}{\sqrt{3 - 2}}$ ，那么12※3＝．

查看试题解析
17. 如图，直线a∥b∥c，直线l₁ ， l₂与这三条平行线分别交于点A，B，C和点D，E，F．若AB：BC=1：2，DE=3，则EF的长为．

查看试题解析
18. 如图，线段AB两端点的坐标分别为A（-1，0），B（1，1），把线段AB平移到CD位置，若线段CD两端点的坐标分别为C（1，a），D（b，4），则a+b的值为

查看试题解析
19. 如图，菱形ABCD的对角线AC、BD相交于点O，E为AD的中点，若OE=3，则菱形ABCD的边长为．

查看试题解析
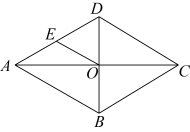20. 如图，为估算某河的宽度，在河对岸选定一个目标点A，在近岸取点B，C，D，使得AB⊥BC，CD⊥BC，点E在BC上，并且点A，E，D在同一条直线上．若测得BE＝20m，EC＝10m，CD＝20m，则河的宽度AB＝m．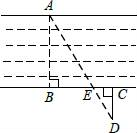

查看试题解析

三、解答题

21. 计算： $\sqrt{12} - \sqrt{20} - \sqrt{27} + \sqrt{45}$ ．

查看试题解析
22. 用适当的方法解下列方程： $x^{2} + 4 x - 5 = 0$ ．

查看试题解析
23. 已知，如图所示，实数a、b、c在数轴上的位置．化简： $\sqrt{a^{2}} - | a - b | + \sqrt{{(c - a)}^{2}} + | b + c |$ ．

查看试题解析
24. 某药品经过两次降价，每瓶零售价由56元降为31.5元．已知两次降价的百分比相同，求每次降价的百分率是多少．

查看试题解析
25. 已知关于x的方程 $x^{2} + k x + k - 3 = 0$ ，求证：不论k取何实数，该方程都有两个不相等的实数根．

查看试题解析
26. 如图，作出与四边形 $A B C D$ 的相似的新四边形，使新图形与原图形的相似比为2：1．

查看试题解析
27. 如图，E是矩形ABCD的边CB上的一点，AF⊥DE于点F．

(1)、求证： $△$ EDC∽ $△$ DAF；

(2)、若AB＝3，AD＝2，CE＝1，求线段DF的长度．

查看试题解析

28. 阅读下列材料，完成相应任务．

直角三角形斜边上的中线等于斜边的一半

如图1，△ABC中， $∠ A B C = 90 °$ ， BD是斜边AC上的中线．求证：BD＝ $\frac{1}{2}$ AC．

分析：要证明BD等于AC的一半，可以用“倍长法”将BD延长一倍，如图2．延长BD到E，使得DE＝BD．

连接AE，CE．可证BE＝AC，进而得到BD＝ $\frac{1}{2}$ AC．

(1)、请你按材料中的分析写出证明过程；

(2)、如图3，点C是线段AB上一点，CD⊥AB，点E是线段CD上一点，分别连接AD，BE，点F，G分别是AD和BE的中点，连接FG．若AB＝12，CD＝8，CE＝3，则

F G =

．

查看试题解析