安徽省芜湖市市区2022-2023学年九年级上学期期中考试数学试题
试卷更新日期:2022-12-01 类型:期中考试
一、单选题
-
1. 一元二次方程x2=-2x的解是( )A、x1=x2=0 B、x1=x2=2 C、x1=0,x2=2 D、x1=0,x2=-22. 用配方法解方程时,原方程应变形为( )A、 B、 C、 D、3. 一元二次方程根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、不能确定4. 在同一平面直角坐标系中作出 , , 的图象,它们的共同点是( )A、关于y轴对称,抛物线的开口向上 B、关于y轴对称,抛物线的开口向下 C、关于y轴对称,抛物线的顶点都是原点 D、当时,y随x的增大而减小5. 若抛物线 , 当时,y随x增大而增大,则a的取值范围是( )A、 B、 C、 D、6. 下列一元二次方程两实数根和为﹣4的是()A、x2+2x﹣4=0 B、x2﹣4x+4=0 C、x2+4x+10=0 D、x2+4x﹣5=07. 受新冠肺炎疫情影响,某企业生产总值从元月份的300万元,连续两个月降至260万元,设平均降低率为x,则可列方程( )A、300(1-x)2=260 B、300(1-x2)=260 C、300(1-2x)=260 D、300(1+x)2=2608. 若抛物线与x轴两个交点之间的距离为4,对称轴为 , 则( )A、 B、 C、 D、9. 汽车在刹车后,由于惯性作用还要继续向前滑行一段距离才能停下,我们称这段距离为“刹车距离”,刹车距离往往跟行驶速度有关,在一个限速35km/h的弯道上,甲、乙两辆汽车相向而行,发现情况不妙,同时刹车,最后还是相撞了事发后,交警现场测得甲车的刹车距离略超过12m,乙车的刹车距离略超过10m,又知甲、乙两种车型的刹车距离s(m)与车速x(km/h)的关系大致如下:S甲 ,S乙 .由此可以推测( )A、甲车超速 B、乙车超速 C、两车都超速 D、两车都未超速10. 如图,在矩形中, , 连接 , 将线段绕着点A顺时针旋转得到 , 则线段的最小值为( )
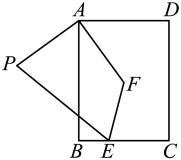 A、 B、 C、4 D、
A、 B、 C、4 D、二、填空题
-
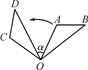
11. 关于x的方程是一元二次方程,则m值为 .12. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数 .
 13. 教练对小明投掷实心球的训练录像进行了技术分析,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为 , 由此可知小明此次投掷的成绩是m.14. 已知二次函数的顶点坐标为 , 则(1)、m+n的值为;(2)、当时,若y的最小值与最大值之和为12,则a的值为 .
13. 教练对小明投掷实心球的训练录像进行了技术分析,发现实心球在行进过程中高度y(m)与水平距离x(m)之间的关系为 , 由此可知小明此次投掷的成绩是m.14. 已知二次函数的顶点坐标为 , 则(1)、m+n的值为;(2)、当时,若y的最小值与最大值之和为12,则a的值为 .三、解答题
-
15. 解方程: .16. 如图,方格纸中每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,已知点C的坐标为 .
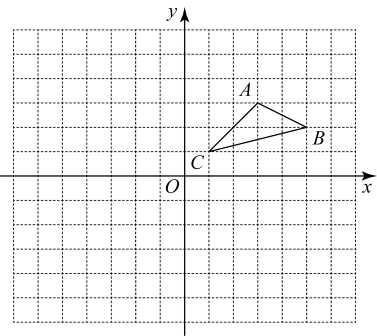 (1)、画出以C为旋转中心,将按顺时针方向旋转后得到的;(2)、画出关于原点O对称的;(3)、设D为x轴上一个动点,且四边形为平行四边形,则点D坐标为 . (直接写出答案)17. 如图,学校课外生物小组的试验园地的形状是长32米、宽20米的长方形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,小道以外的区域用于种植有关植物,要使种植总面积为570平方米,则小道的宽为多少米?
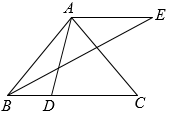
(1)、画出以C为旋转中心,将按顺时针方向旋转后得到的;(2)、画出关于原点O对称的;(3)、设D为x轴上一个动点,且四边形为平行四边形,则点D坐标为 . (直接写出答案)17. 如图,学校课外生物小组的试验园地的形状是长32米、宽20米的长方形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,小道以外的区域用于种植有关植物,要使种植总面积为570平方米,则小道的宽为多少米?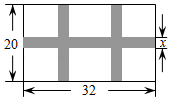 18. 如图,将矩形绕点A顺时针旋转得到矩形 , 点C的对应点恰好落在的延长线上,求证: .
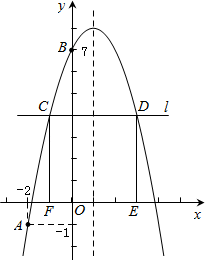
18. 如图,将矩形绕点A顺时针旋转得到矩形 , 点C的对应点恰好落在的延长线上,求证: .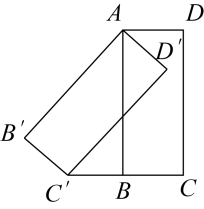 19. 已知关于x的方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一个根大于4且小于8,求m的取值范围.20. 先将二次函数的图象向右平移2个单位,再向上平移8个单位,所得图象与x轴相交于点A和点B.(1)、求线段的长;(2)、设直线与的图象交于Q点,当的面积为18时,试确定Q点的坐标.21. 小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量 (本)与销售单价 (元)之间满足一次函数关系,三对对应值如下表:
19. 已知关于x的方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一个根大于4且小于8,求m的取值范围.20. 先将二次函数的图象向右平移2个单位,再向上平移8个单位,所得图象与x轴相交于点A和点B.(1)、求线段的长;(2)、设直线与的图象交于Q点,当的面积为18时,试确定Q点的坐标.21. 小红经营的网店以销售文具为主,其中一款笔记本进价为每本10元,该网店在试销售期间发现,每周销售数量 (本)与销售单价 (元)之间满足一次函数关系,三对对应值如下表:销售单价 (元)
12
14
16
每周的销售量 (本)
500
400
300
(1)、求 与 之间的函数关系式;(2)、通过与其他网店对比,小红将这款笔记本的单价定为 元( ,且 为整数),设每周销售该款笔记本所获利润为 元,当销售单价定为多少元时每周所获利润最大,最大利润是多少元?