北京市通州区2022-2023学年九年级上学期期中数学试卷
试卷更新日期:2022-12-01 类型:期中考试
一、单选题
-
1. 已知2x=3y(xy≠0),那么下列比例式中成立的是( )A、 B、 C、 D、2. 下列点坐标,是二次函数图象的顶点坐标的是( )A、(2,4) B、 C、 D、)3. 下列判断正确的是( )A、任意两个平行四边形一定相似 B、任意两个矩形一定相似 C、任意两个菱形一定相似 D、任意两个正方形一定相似4. 如图,在 , . 将沿图中的剪开.剪下的阴影三角形与原三角形不相似的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 把二次函数的图象向左平移2个单位,然后向上平移1个单位,则平移后的图象对应的二次函数的表达式为( )A、 B、 C、 D、6. 已知点都在函数的图像上,则下列结论正确的是( )A、 B、 C、 D、7. 如图,小亮的数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.m,测得AB=2m,BC=14m,则旗杆CD高度是( )
5. 把二次函数的图象向左平移2个单位,然后向上平移1个单位,则平移后的图象对应的二次函数的表达式为( )A、 B、 C、 D、6. 已知点都在函数的图像上,则下列结论正确的是( )A、 B、 C、 D、7. 如图,小亮的数学兴趣小组利用标杆BE测量学校旗杆CD的高度,标杆BE高1.m,测得AB=2m,BC=14m,则旗杆CD高度是( ) A、9m B、10.m C、12m D、16m8. 如图,在中,点E是边上的点,线段与交于点F,如果 , 那么的长是( )
A、9m B、10.m C、12m D、16m8. 如图,在中,点E是边上的点,线段与交于点F,如果 , 那么的长是( ) A、3 B、6 C、9 D、129. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、3 B、6 C、9 D、129. 一次函数y=ax+b(a≠0)与二次函数y=ax2+bx+c(a≠0)在同一平面直角坐标系中的图象可能是( )
A、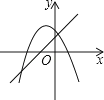 B、
B、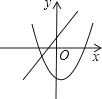 C、
C、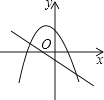 D、
D、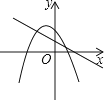 10. 在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大.收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”P的可能性最大的线路是( )
10. 在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大.收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”P的可能性最大的线路是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,在中, , 点D在上(不与点A,C重合),只需添加一个条件即可证明和相似,这个条件可以是(写出一个即可).
 12. 如图,直线l1∥l2∥l3 , 直线l4 , l5被直线l1、l2、l3所截,截得的线段分别为AB,BC,DE,EF,若AB=4,BC=6,DE=3,则EF的长是 .
12. 如图,直线l1∥l2∥l3 , 直线l4 , l5被直线l1、l2、l3所截,截得的线段分别为AB,BC,DE,EF,若AB=4,BC=6,DE=3,则EF的长是 . 13. 若二次函数的图象与x轴有一个公共点,则k=14. 已知二次函数 , 将这个二次函数表达式用配方法化成的形式 .15. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是cm.
13. 若二次函数的图象与x轴有一个公共点,则k=14. 已知二次函数 , 将这个二次函数表达式用配方法化成的形式 .15. 据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了世界上第1个“小孔成像”的实验,阐释了光的直线传播原理,如图(1)所示。如图(2)所示的小孔成像实验中,若物距为10cm,像距为15cm,蜡烛火焰倒立的像的高度是6cm,则蜡烛火焰的高度是cm. 16. 某工厂今年八月份医用防护服的产量是50万件,计划九月份和十月份增加产量,如果月平均增长率为x,那么十月份医用防护服的产量y(万件)与x之间的函数表达式为 .17. 如图,在中,是斜边上的高.如果 , 那么的长为 .
16. 某工厂今年八月份医用防护服的产量是50万件,计划九月份和十月份增加产量,如果月平均增长率为x,那么十月份医用防护服的产量y(万件)与x之间的函数表达式为 .17. 如图,在中,是斜边上的高.如果 , 那么的长为 . 18. 若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为 .
18. 若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为 .三、解答题
-
19. 已知是二次函数图象上两点,求二次函数的表达式.20. 如图,AC,BD相交于的点O,且∠ABO=∠C.求证:△AOB∽△DOC.
 21. 如图,是小凯为估算鱼塘的宽AB设计的,在陆地上取点 , 使得在同一条直线上,在同一条直线上,测得 . 小凯测得的长为10米,求鱼塘的宽的长是多少米?
21. 如图,是小凯为估算鱼塘的宽AB设计的,在陆地上取点 , 使得在同一条直线上,在同一条直线上,测得 . 小凯测得的长为10米,求鱼塘的宽的长是多少米? 22. 已知:如图,线段AB.
22. 已知:如图,线段AB.
求作:点C,D,使得点C,D在线段AB上,且AC=CD=DB.
作法:①作射线AM,在射线AM上顺次截取线段AE=EF=FG,连接BG;
②以点E为圆心,BG长为半径画弧,再以点B为圆心,EG长为半径画弧,两弧在AB上方交于点H;
③连接BH,连接EH交AB于点C,在线段CB上截取线段CD=AC.
所以点C,D就是所求作的点.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵EH=BG,BH=EG,
∴四边形EGBH是平行四边形.( )(填推理的依据)
∴ , 即 .
∴AC∶_▲_=AE∶AG.
∵AE=EF=FG,
∴AE=_▲_AG.
∴ .
∴ .
∴AC=CD=DB.
23. 已知一个二次函数图象上部分点的横坐标x与纵坐标y的对应值如表所示:
x
……
-3
-2
-1
0
1
……
y
……
0
3
4
3
0
……
(1)、求这个二次函数的表达式;(2)、在给定的平面直角坐标系中画出这个二次函数的图象;(3)、当-2≤x<2时,直接写出y的取值范围.24. 如图,AB⊥BC,EC⊥BC,点D在BC上,AB=1,BD=2,CD=3,CE=6. (1)、求证:△ABD∽△DCE;(2)、求∠ADE的度数.25. 在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=1,且其顶点在直线y=-2x-2上.
(1)、求证:△ABD∽△DCE;(2)、求∠ADE的度数.25. 在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=1,且其顶点在直线y=-2x-2上. (1)、求抛物线的顶点坐标;(2)、求抛物线的解析式;(3)、在给定的平面直角坐标系中画出这个二次函数的图象.26. 小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为x轴方向,1m为单位长度,建立了如图所示的平面直角坐标系,铅球从y轴上的A点出手,运动路径可看作抛物线,在B点处达到最高位置,落在x轴上的点C处.小明某次试投时的数据如图所示.
(1)、求抛物线的顶点坐标;(2)、求抛物线的解析式;(3)、在给定的平面直角坐标系中画出这个二次函数的图象.26. 小明进行铅球训练,他尝试利用数学模型来研究铅球的运动情况.他以水平方向为x轴方向,1m为单位长度,建立了如图所示的平面直角坐标系,铅球从y轴上的A点出手,运动路径可看作抛物线,在B点处达到最高位置,落在x轴上的点C处.小明某次试投时的数据如图所示.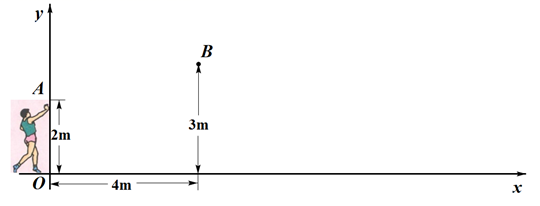 (1)、在图中画出铅球运动路径的示意图;(2)、根据图中信息,求出铅球路径所在抛物线的表达式;(3)、若铅球投掷距离(铅球落地点C与出手点A的水平距离 的长度)不小于10m,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.27. 如图,中, , , 过点A的射线与斜边交于点D,且满足 , 于点E,求证: .
(1)、在图中画出铅球运动路径的示意图;(2)、根据图中信息,求出铅球路径所在抛物线的表达式;(3)、若铅球投掷距离(铅球落地点C与出手点A的水平距离 的长度)不小于10m,成绩为优秀.请通过计算,判断小明此次试投的成绩是否能达到优秀.27. 如图,中, , , 过点A的射线与斜边交于点D,且满足 , 于点E,求证: . 28. 给出如下规定:两个图形和 , 点P为上任一点,点Q为上任一点,如果线段的长度存在最小值,就称该最小值为两个图形和之间的距离.
28. 给出如下规定:两个图形和 , 点P为上任一点,点Q为上任一点,如果线段的长度存在最小值,就称该最小值为两个图形和之间的距离.在平面直角坐标系中,O为坐标原点.
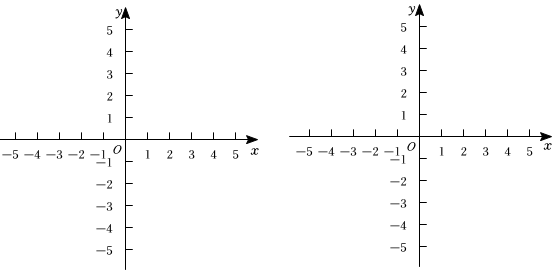 (1)、点A的坐标为 , 则点和射线之间的距离为 , 点和射线之间的距离为 .(2)、点E的坐标为 , 将射线绕原点O逆时针旋转 , 得到射线 , 在坐标平面内所有和射线之间的距离相等的点所组成的图形记为图形M.
(1)、点A的坐标为 , 则点和射线之间的距离为 , 点和射线之间的距离为 .(2)、点E的坐标为 , 将射线绕原点O逆时针旋转 , 得到射线 , 在坐标平面内所有和射线之间的距离相等的点所组成的图形记为图形M.①在坐标系中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)
②将抛物线与图形M的公共部分记为图形N,射线 , 组成的图形记为图形W,请直接写出图形W和图形N之间的距离.