广东省清远市阳山县2022-2023学年九年级上学期期中教学质量检查数学练习题

试卷更新日期：2022-12-01 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，是一元二次方程的是（）

A、 $2 x^{2} + x + 1$ B、 $x^{2} + \frac{1}{x} + 2 = 0$ C、 $x^{2} + 2 x y - 3 = 0$ D、 $\frac{3}{7} x^{2} = 0$

查看试题解析
2. 既是中心对称图形又是轴对称图形，且只有两条对称轴的四边形是（）

A、正方形 B、矩形 C、菱形 D、矩形或菱形

查看试题解析
3. 下列性质中，菱形具有而矩形不一定具有的是（　　）

A、对边平行且相等 B、对角线互相平分 C、对角线相等 D、对角线互相垂直

查看试题解析
4. 用配方法解一元二次方程x²﹣8x﹣11=0时，下列变形正确的是（）

A、（x﹣4）²=5 B、（x+4）²=5 C、（x﹣4）²=27 D、（x+4）²=27

查看试题解析
5. 在一个不透明的布袋中装有红色.白色玻璃球共40个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到白色球的频率稳定在85％左右，则口袋中红色球可能有（）.

A、34个 B、30个 C、10个 D、6个

查看试题解析
6. 如图，在矩形 $A B C D$ 中，两条对角线相交于点O， $∠ A O D = 120 °$ ， $A B = 2$ ，矩形的面积是（）

A、 $2 \sqrt{3}$ B、 $4 \sqrt{3}$ C、8 D、12

查看试题解析
7. 某种品牌运动服经过两次降价，每件零售价由 $560$ 元降为 $315$ 元，已知两次降价的百分率相同，求每次降价的百分率，设每次降价的百分率为x，下面所列的方程中正确的是（）

A、 $560 {(1 + x)}^{2} = 315$ B、 $560 (1 - x^{2}) = 315$ C、 $560 (1 - 2 x) = 315$ D、 $560 {(1 - x)}^{2} = 315$

查看试题解析
8. 关于x的一元二次方程x²－4x＋2=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、有无实数根，无法判断

查看试题解析
9. 如图，菱形ABCD的对角线AC，BD相交于点O，E，F分别是AB，BC边上的中点，连接EF.若 $E F = \sqrt{3}$ ，BD=4，则菱形ABCD的周长为（）

A、4 B、 $4 \sqrt{6}$ C、 $4 \sqrt{7}$ D、28

查看试题解析
10. 如图，四边形 $A B C D$ 中，E、F、G、H分别是 $A B$ 、 $D C$ 、 $C A$ 、 $D B$ 的中点，若中点四边形 $E H F G$ 是菱形，那么原四边形 $A B C D$ 满足什么条件（）

A、 $A D = B C$ B、 $A C ⊥ B D$ C、 $A C = B D$ D、 $∠ D A B + ∠ A B C = 90 °$

查看试题解析

二、填空题

11. 一元二次方程 $x^{2} - 2 x = 0$ 的解是

查看试题解析
12. 若关于x的一元二次方程 $x^{2} – x – m = 0$ 的一个根是x=1，则m的值是．

查看试题解析
13. 重庆市某校初二（3）班同学，在学校组织的语文作文选拔考试中，有三名同学满分，其中有一名男生和两名女生，现在从三名满分同学中随机抽取两名同学参加重庆市优秀作文比赛，则选出来的两名同学刚好是一男一女的概率是.

查看试题解析
14. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O，添加一个条件，使菱形 $A B C D$ 是正方形．

查看试题解析
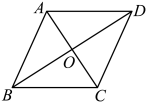15. 已知方程 $x^{2} - 10 x + 24 = 0$ 的两个根为等腰三角形（非等边）边长，则等腰三角形的周长为．

查看试题解析
16. 如图，为美化中心城区环境，政府计划在长为30米，宽为20米的矩形场地 $A B C D$ 上修建公园，其中要留出宽度相等的三条小路，且两条与 $A B$ 平行，另一条与 $A D$ 平行，其余部分造成花圃．若花圃总面积为448平方米，若设小路宽为x米，根据题意可列方程得：．

查看试题解析
17. 如图，菱形ABCD中，对角线AC与BD相交于点O，且AC=8，BD=6，则菱形ABCD的高DH= ．

查看试题解析

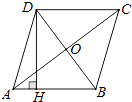
三、解答题

18. 解一元二次方程： $x^{2} + 4 x - 3 = 0$ ．

查看试题解析
19.
已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．

查看试题解析
20. 一个不透明的口袋里装有分别标有汉字“我”、“爱”、“中”、“国”的四个小球，除汉字不同之外，小球没有任何区别.每次摸球前先搅拌均匀.先从中任取一球，不放回，再从中任取一球，请用树状图或列表的方法，求取出的两个球上的汉字能组成“中国”的概率.

查看试题解析
21. 一商店销售某种商品，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，该店采取了降价措施．在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

(1)、如果每件盈利30元，平均每天可售出多少件？

(2)、当每件商品降价多少元时，该商店每天销售利润为1050元？

查看试题解析
22. 如图，在Rt△ABC中，∠ACB=90°，点D是斜边AB的中点，过点B、点C分别作BE∥CD，CE∥BD．

(1)、求证：四边形BECD是菱形；

(2)、若∠A=60°，AC= $\sqrt{3}$ ，求菱形BECD的面积.

查看试题解析
23. 已知关于x的一元二次方程 $x^{2} + (m + 2) x + m + 1 = 0$ ．

(1)、求证：无论m取何值，原方程总有两个实数根；

(2)、若方程的一个根为-2，求m的值及方程的另一个根．

查看试题解析
24. 如图，正方形 $A B C D$ 和正方形 $A E F G$ 有公共点A，点B在线段 $D G$ 上，

(1)、求证： $△ A D G ≌ △ A B E$ ；

(2)、判断 $D G$ 与 $B E$ 的位置关系，并说明理由．

查看试题解析
25. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 11 c m$ ， $B C = 8 c m$ ，点P从点A出发，以每秒1cm的速度沿 $A B$ 向点B匀速运动，同时点Q从点B出发以每秒2cm的速度沿 $B C$ 向点C匀速运动，到达点C后返回点B，当有一点停止运动时，另一点也停止运动，设运动时间为t秒．

(1)、当 $t = 1$ 时，直接写出P，Q两点间的距离．

(2)、是否存在t，使得 $△ B P Q$ 是等腰三角形，若存在，请求出t的值；若不存在，请说明理由．

(3)、是否存在t，使得 $△ B P Q$ 的面积等于 $10 c m^{2}$ ，若存在，请求出t的值：若不存在，请说明理由．

查看试题解析