吉林省白城市大安市2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-01 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若抛物线与的形状相同,则a的值为( )A、 B、 C、 D、3. 下列关于x的一元二次方程中,有两个相等的实数根的是( )A、 B、 C、 D、4. 如图,将绕着点O顺时针旋转,得到(点C落在外),若 , , 则最小旋转角度是( )
2. 若抛物线与的形状相同,则a的值为( )A、 B、 C、 D、3. 下列关于x的一元二次方程中,有两个相等的实数根的是( )A、 B、 C、 D、4. 如图,将绕着点O顺时针旋转,得到(点C落在外),若 , , 则最小旋转角度是( ) A、20° B、30° C、40° D、50°5. 如图,C、D是上直径两侧的点,若 , 则等于( )
A、20° B、30° C、40° D、50°5. 如图,C、D是上直径两侧的点,若 , 则等于( ) A、 B、 C、 D、6. 如图,已如抛物线 开口向上,与 轴的一个交点为 ,对称轴为直线 .下列结论错误的是( )
A、 B、 C、 D、6. 如图,已如抛物线 开口向上,与 轴的一个交点为 ,对称轴为直线 .下列结论错误的是( )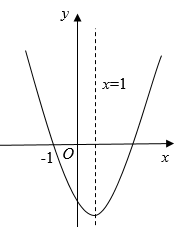 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 在平面直角坐标系中,若点与点关于原点对称,则m的值是 .8. 抛物线的顶点坐标是 .9. 如图所示,这个图案绕精它的中心旋转α()后能够与它本身重合,则α可以为 (写出一个即可).
 10. 已知点 、、都在函数的图象上,则、、的大小关系为 (用“”连接).11. 数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为cm.
10. 已知点 、、都在函数的图象上,则、、的大小关系为 (用“”连接).11. 数学活动课上,小东想测算一个圆形齿轮内圈圆的半径.如图所示,小东首先在内圈圆上取点A,B,再作弦AB的垂直平分线,垂足为C,交于点D,连接CD,经测量cm,cm,那么这个齿轮内圈圆的半径为cm.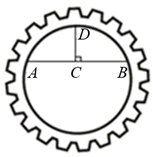 12. 如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,若点A的坐标为(-4,-3),则点A′的坐标为 .
12. 如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,若点A的坐标为(-4,-3),则点A′的坐标为 . 13. 如图,四边形内接于 , 是它的一个外角,若 , 则度.
13. 如图,四边形内接于 , 是它的一个外角,若 , 则度. 14. 如图,在平面直角坐标系中,抛物线与x轴交于点A、B,与y轴交于点C,过点C作轴,交抛物线于另一点D,若 , 则c的值为 .
14. 如图,在平面直角坐标系中,抛物线与x轴交于点A、B,与y轴交于点C,过点C作轴,交抛物线于另一点D,若 , 则c的值为 .
三、解答题
-
15. 解方程: .16. 在平面直角坐标系中,求抛物线与x轴的交点坐标.17. 某市2019年底,城市树木花草的绿化面积约350万亩,为持续保护和改善生态环境,经过两年的努力,到2021年底绿化面积约423.5万亩.求这两年绿化面积的年平均增长率.18. 如图,将绕点A逆时针旋转得到 . 使点B的对应点E落在边上,求的度数.
 19. 图1、图2、图3均为5×5的正方形网格,每个小正方形的顶点称为格点,的顶点和点D均在格点上,仅用无刻度的直尺,在给定的网格中,按下列要求面图、并保留作图痕迹、
19. 图1、图2、图3均为5×5的正方形网格,每个小正方形的顶点称为格点,的顶点和点D均在格点上,仅用无刻度的直尺,在给定的网格中,按下列要求面图、并保留作图痕迹、
( 1 )在图1中,画出将绕点D顺时针旋转90°得到的
( 2 )在图2中,画出使与关于点D成中心对称;
( 3 )在图3中,以AB为一边画出一个、使的面积是的面积的4倍.
20. 如图,正常水位时,抛物线形拱桥下的水面宽AB为 , 此时拱桥的最高点到水面的距离为 . (1)、把拱桥看作一个二次函数的图象,建立恰当的平面直角坐标系,求出这个二次函数的表达式;(2)、当水面宽时,达到警戒水位,如果水位以的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没?21. 如图,在中,B、C是的三等分点,弦相交于点E.
(1)、把拱桥看作一个二次函数的图象,建立恰当的平面直角坐标系,求出这个二次函数的表达式;(2)、当水面宽时,达到警戒水位,如果水位以的速度持续上涨,那么达到警戒水位后,再过多长时间此桥孔将被淹没?21. 如图,在中,B、C是的三等分点,弦相交于点E.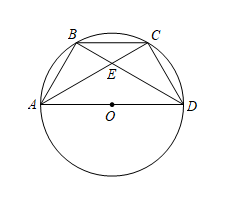 (1)、求证:;(2)、连接 , 若 , 求的度数.22. 如图,在平面直角坐标系中,抛物线:的图象经过点、 , 与y轴交于点C.
(1)、求证:;(2)、连接 , 若 , 求的度数.22. 如图,在平面直角坐标系中,抛物线:的图象经过点、 , 与y轴交于点C. (1)、求抛物线的解析式;(2)、将抛物线先向左平移3个单位长度,再向下平移2个单位长度后得到抛物线 , 抛物线的顶点为D,求的面积.23. 如图,用的篙色围成一个边靠墙的矩形场地,墙长 . 垂直于墙的边长为 . 围成的矩形场地的面积为 .
(1)、求抛物线的解析式;(2)、将抛物线先向左平移3个单位长度,再向下平移2个单位长度后得到抛物线 , 抛物线的顶点为D,求的面积.23. 如图,用的篙色围成一个边靠墙的矩形场地,墙长 . 垂直于墙的边长为 . 围成的矩形场地的面积为 . (1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、求这个矩形场地面积的最大值.24.
(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、求这个矩形场地面积的最大值.24. (1)、[猜想]如图1,在中,点C在优弧上,连接 , 得到圆心角 , 发现,与对着同一条弧 , 则;
(1)、[猜想]如图1,在中,点C在优弧上,连接 , 得到圆心角 , 发现,与对着同一条弧 , 则;[特例探究]为证明图1中的结论,我们不妨使点O在的边上,如图2.若 , 则度;
(2)、[证明结论]请结合图2的特例探究,用图1证明[猜想]中的结论;(3)、结论应用]在图1中,若 , 点P在上,且是等腰三角形,直接写出该等腰三角形的顶角的度数.25. [操作]如图1.是等腰直角三角形, , D是其内部的一点,连接 . 将绕点(顺时针旋转90°得到 , 连接 , 作直线交于点F. (1)、求证:;(2)、求的度数;(3)、[探究]如图2,连接图1中的 , 分别取的中点M、N、P,作 . 若 , 则的周长为26. 如图,在平面直角坐标系中,点在抛物线上,其对称轴是直线 . 点P、Q为该抛物线上的点,其横坐标分别为m, , 设该抛物线在点P与点Q之间部分(含点P和点Q)的图象记为G,图象G的最高点与最低点的纵坐标之差为h.
(1)、求证:;(2)、求的度数;(3)、[探究]如图2,连接图1中的 , 分别取的中点M、N、P,作 . 若 , 则的周长为26. 如图,在平面直角坐标系中,点在抛物线上,其对称轴是直线 . 点P、Q为该抛物线上的点,其横坐标分别为m, , 设该抛物线在点P与点Q之间部分(含点P和点Q)的图象记为G,图象G的最高点与最低点的纵坐标之差为h. (1)、求该抛物线的解析式;(2)、点P的纵坐标为2时,求点Q的坐标;(3)、当图象G的最低点是该抛物线的顶点时,①求h与m之间的函数关系式;②当时,直接写出m的值.
(1)、求该抛物线的解析式;(2)、点P的纵坐标为2时,求点Q的坐标;(3)、当图象G的最低点是该抛物线的顶点时,①求h与m之间的函数关系式;②当时,直接写出m的值.