山东省临沂市罗庄区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-12-01 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列说法正确的是( )A、的项是 , 2 B、是二次三项式 C、与是同类项 D、单项式的系数是4. 下列叙述正确的是( )A、线段AB可表示为线段BA B、射线AB可表示为射线BA C、直线可以比较长短 D、射线可以比较长短5. 已知 ,那么下列关系正确的是( )A、 B、 C、 D、6. 如图,已知线段AB=10cm,M是AB中点,点N在AB上,NB=2cm,那么线段MN的长为( )
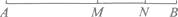 A、5cm B、4cm C、3cm D、2cm7. 如图,点O是直线上的一点,若 , , , 下列正确的是( )
A、5cm B、4cm C、3cm D、2cm7. 如图,点O是直线上的一点,若 , , , 下列正确的是( )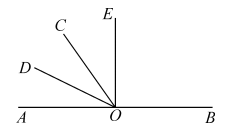 A、 B、 C、 D、8. 已知关于x的多项式为二次三项式,则当时,这个二次三项式的值是( )A、7 B、6 C、4 D、39. 张老师有一批屯册准备分给苦干个小朋友,如果每3人分到一本,那么还剩2本;如果每2人分到一本,那么还有9人没有分到.设小朋友的人数为 人,则可以列出方程是( )A、 B、 C、 D、10. 如图,数轴上A,B两点对应的数分别是a和b,对于以下四个式子: , , , , 其中值为负数的个数是( )
A、 B、 C、 D、8. 已知关于x的多项式为二次三项式,则当时,这个二次三项式的值是( )A、7 B、6 C、4 D、39. 张老师有一批屯册准备分给苦干个小朋友,如果每3人分到一本,那么还剩2本;如果每2人分到一本,那么还有9人没有分到.设小朋友的人数为 人,则可以列出方程是( )A、 B、 C、 D、10. 如图,数轴上A,B两点对应的数分别是a和b,对于以下四个式子: , , , , 其中值为负数的个数是( )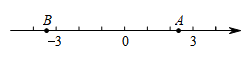 A、4 B、3 C、2 D、111. 若方程和的解相同,则的值为( )A、 B、2 C、 D、12. 如图所示,在这个数据运算程序中,若开始输入的的值为2,结果输出的是1,返回进行第二次运算则输出的是 , , 则第2021次输出的结果是( )
A、4 B、3 C、2 D、111. 若方程和的解相同,则的值为( )A、 B、2 C、 D、12. 如图所示,在这个数据运算程序中,若开始输入的的值为2,结果输出的是1,返回进行第二次运算则输出的是 , , 则第2021次输出的结果是( )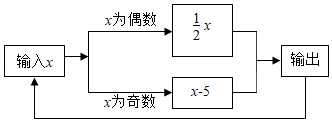 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知 , 则的补角的度数为 .14. 若单项式与是同类项,则的值是 .15. 在射线上截取线段 , , 点M,N分别是 , 的中点,则点M和点N之间的距离为 .16. 若有理数a,b,c在数轴上的位置如图所示,则化简: .
 17. 已知 , 则的值为 .18. 一块手表上午11:10时针和分针所夹锐角的度数是.19. 对于两个数a,b,我们规定用表示这两个数的平均数,用表示这两个数中最小的数,例如: , , 如果 , 那么 .20. 如图,数轴上有一点C,满足则C表示的数是(用含m的式子表示).
17. 已知 , 则的值为 .18. 一块手表上午11:10时针和分针所夹锐角的度数是.19. 对于两个数a,b,我们规定用表示这两个数的平均数,用表示这两个数中最小的数,例如: , , 如果 , 那么 .20. 如图,数轴上有一点C,满足则C表示的数是(用含m的式子表示).
三、解答题
-
21. 计算:(1)、(2)、22. 解方程(1)、(2)、23. 先化简,再求值: , 其中 , .