山东省临沂市兰山区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. 计算-3²的值是

A、9 B、-9 C、6 D、-6

查看试题解析
2. 中国信息通信研究院指出5G对经济社会发展的影响力开始显现，据统计2020年5G将直接带动经济总产出约为8109亿元，将810900000000用科学记数法表示应为（）

A、 $8.109 \times 10^{10}$ B、 $8.109 \times 10^{11}$ C、 $81.09 \times 10^{10}$ D、 $0.8109 \times 10^{12}$

查看试题解析
3. 下列计算正确的是（）

A、3a+4=7ab B、7x﹣3x=4 C、3m+m=3m² D、3x²y﹣2x²y=x²y

查看试题解析
4. 下列各式运用等式的性质变形，错误的是（）

A、若 $- a = - b$ ，则 $a = b$ B、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ C、若 $a c = b c$ ，则 $a = b$ D、若 $(m^{2} + 1) a = (m^{2} + 1) b$ ，则 $a = b$

查看试题解析
5. 下列说法正确的个数有（）
①-0.5x³y²与2y²x³是同类项
②单项式 $- \frac{2 π x^{2} y^{3}}{3}$ 的次数是5次，系数是 $- \frac{2}{3}$
③若|a|＝-a，则a＜0
④a²b²-2a+3是四次三项式

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 若关于x的方程2x-kx+1＝-2的解为x＝-1，则k的值为（）

A、-1 B、-4 C、-6 D、-8

查看试题解析
7. 下面说法正确的是（）

A、两点之间，直线最短 B、连接两点的线段叫做两点间的距离 C、一个锐角的补角比这个角的余角大90° D、若∠AOC＝ $\frac{1}{2}$ ∠AOB，则OC是∠AOB的平分线

查看试题解析
8. 下列方程变形中，正确的是（）

A、由3x-2＝2x+1，得3x-2x＝-1+2 B、由3-x＝2-5（x-1），得3-x＝2-5x-1 C、由6x＝3，得x＝2 D、由 $\frac{1}{2}$ x+1＝ $\frac{2}{3}$ x-2，得3x+6＝4x-12

查看试题解析
9. 轮船沿江从 $A$ 港顺流行驶到 $B$ 港，比从 $B$ 港返回 $A$ 港少用3小时，若船速为26千米/时，水速为2千米/时，求 $A$ 港和 $B$ 港相距多少千米. 设 $A$ 港和 $B$ 港相距 $x$ 千米. 根据题意，可列出的方程是（）.

A、 $\frac{x}{28} = \frac{x}{24} - 3$ B、 $\frac{x}{28} = \frac{x}{24} + 3$ C、 $\frac{x + 2}{26} = \frac{x - 2}{26} + 3$ D、 $\frac{x + 2}{26} = \frac{x - 2}{26} - 3$

查看试题解析
10. 植物园内，月季花按正方形种植，在它的周围种植牵牛花，如图反映了月季花的列数（n）和牵牛花的数量规律，那么当n＝2021时，牵牛花的数量为（）

A、8076株 B、8080株 C、8084株 D、8088株

查看试题解析

二、填空题

11. －0.25的倒数是.

查看试题解析
12. 已知x²-2x-8＝0，则代数式2x²-4x-10＝．

查看试题解析
13. 已知一个角的补角比这个角的余角的3倍大 $10 °$ ，则这个角的度数为．

查看试题解析
14. 一项工程甲单独做需要10天完成，乙单独做需要8天完成．若甲先做1天，然后由甲、乙合作完成此项工程，则甲一共做了天．

查看试题解析
15. 如图，A，O，B三点在同一条直线上，点A在点O的北偏西67°的方向上，点D在正北方向上，则∠BOD的度数是．

查看试题解析
16. 如图，将三个同样的直角三角尺的直角顶点重合放置，那么∠AOB的度数为．

查看试题解析
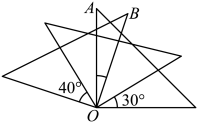17. 已知如右图：点A在数轴上的位置如图所示，点B也在数轴上，且A、B两点之间的距离是2，则点B表示的数是.

查看试题解析
18. 我们定义：若两个角差的绝对值等于 $60^{\circ}$ ，则称这两个角互为“正角”，其中一个角是另一个角的“正角”，如： $∠ 1 = 110^{\circ}$ ， $∠ 2 = 50^{\circ}$ ， $| ∠ 1 - ∠ 2 | = 60^{\circ}$ ，则 $∠ 1$ 和 $∠ 2$ 互为“正角”.如图，已知 $∠ A O B = 120^{\circ}$ ，射线 $O C$ 平分 $∠ A O B$ ， $∠ E O F$ 在 $∠ A O B$ 的内部，若 $∠ E O F = 60^{\circ}$ ，则图中互为“正角”的共有对.

查看试题解析

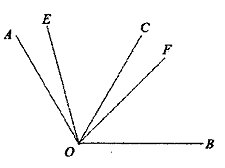
三、解答题

19. 计算：-（-1）²- $\frac{1}{3}$ ×[2+（-5）²]．

查看试题解析
20. 先化简再求值：2（6x²-9xy）-3（4x²-7xy），其中x，y满足|x-1|+（y+2）²＝0．

查看试题解析
21. 解下列方程：

(1)、 $x - 4 = 3 (2 x - 3)$ ；

(2)、 $x - \frac{x - 1}{2} = \frac{x + 2}{3} + 1$ ．

查看试题解析
22. 某糕点厂中秋节前要制作一批盒装月饼，每盒中装2块大月饼和4块小月饼．制作1块大月饼要用0.05kg面粉，1块小月饼要用0.02kg面粉．现共有面粉4500kg，问制作两种月饼应各用多少面粉，才能生产最多的盒装月饼？（用一元一次方程解答）

查看试题解析
23. 如图，点C是线段AB上的一点，点M是线段AC的中点，点N是线段BC的中点．

(1)、如果AB＝12cm，AM＝5cm，求BC的长；

(2)、如果MN＝8cm，求AB的长．

查看试题解析
24. 甲、乙两家超市以相同的价格出售同样的商品，为了吸引顾客，各自推出不同的优惠方案：在甲超市累计购买商品超出300元之后，超出部分按原价8折优惠；在乙超市累计购买商品超出200元之后，超出部分按原价8.5折优惠．设顾客预计累计购物x元（x＞300）．

(1)、请用含x代数式分别表示顾客在两家超市购物所付的费用；

(2)、李明准备购买500元的商品，你认为他应该去哪家超市？请说明理由．

(3)、计算一下，李明购买多少元的商品时，到两家超市购物所付的费用一样？

查看试题解析
25. 如图，以直线AB上一点O为端点作射线OC，将一块直角三角板的直角顶点放在O处．（注：∠DOE＝90°）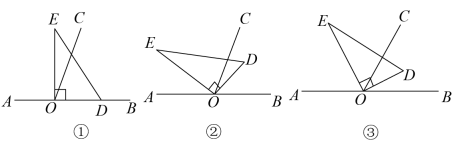

(1)、如图①，若直角三角板DOE的一边OD放在射线OB上，且∠BOC＝70°，则∠COE＝°；

(2)、如图②，将直角三角板DOE绕点O逆时针方向转动到某个位置时，∠BOC＝70°，使OD在∠BOC内部，且满足∠AOE＝5∠COD，求∠BOD的度数；

(3)、如图③，将直角三角板DOE绕点O逆时针方向转动到如图所示位置时，若OE恰好平分∠AOC，试说明OD所在射线是∠BOC的平分线．

查看试题解析