山东省临沂市莒南县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. 2的相反数是（）

A、2 B、－2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 根据县级生产总值统一核算结果，2020年临沭县生产总值初步核算数据为29658000000元，用科学记数法表示为（）

A、 $2.9658 \times 1 0^{8}$ B、 $2.9658 \times 1 0^{9}$ C、 $2.9658 \times 1 0^{10}$ D、 $29.658 \times 1 0^{10}$

查看试题解析
3. 已知a，b，c是三个有理数，它们在数轴上的位置如图所示，化简|a﹣b|+|c﹣a|﹣|b+c|得（）

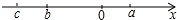A、2c﹣2b B、﹣2a C、2a D、﹣2b

查看试题解析
4. 方程 $2 - \frac{3 x - 7}{4} = - \frac{x + 17}{5}$ 去分母得（）.

A、2-5(3x-7)=-4(x+17) B、40-15x-35=-4x-68 C、40-5(3x-7)=-4x+68 D、40-5(3x-7)=-4(x+17)

查看试题解析
5. 如图，OC是∠AOB的平分线，∠BOD＝ $\frac{1}{2}$ ∠COD，∠BOD＝20°，则∠AOB的度数为（）

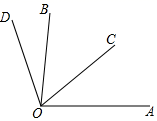A、100° B、80° C、60° D、40°

查看试题解析
6. 如图所示，下列说法错误的是（）

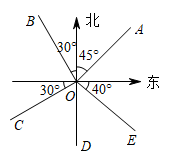A、射线OA表示东北方向 B、射线OB表示北偏西30° C、射线OC表示南偏西60° D、射线OE表示南偏东40°

查看试题解析
7. 下列利用等式的性质，错误的是（）

A、由a=b，得到1-a=1-b B、由 $\frac{a}{2} = \frac{b}{2}$ ，得到a=b C、由a=b，得到ac=bc D、由ac=bc，得到a=b

查看试题解析
8. 下列说法正确的是（）

A、 $2^{3} a^{4}$ 的系数是2，次数是7 B、若 $- \frac{3}{4} x^{m} y^{2}$ 的次数是5，则m=5 C、0不是单项式 D、若 $x^{2} + m x$ 是单项式，则m=0或 $x$ =0

查看试题解析
9. 多项式 $8 x^{2} - 3 x + 5$ 与多项式 $3 x^{3} + 2 m x^{2} - 5 x + 7$ 相加后，不含二次项，则常数m的值是（）

A、2 B、 $- 4$ C、 $- 2$ D、 $- 8$

查看试题解析
10. 已知 $x = 2$ 是关于 $x$ 的一元一次方程 $a x + 1 = 5$ 的解，那么 $a$ 的值为（）

A、 $- 3$ B、 $- 2$ C、 $2$ D、 $3$

查看试题解析
11. 如图所示的几何体是由五个小正方体组成的，它的左视图是（）

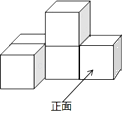A、 B、 C、 D、

查看试题解析
12. 如图，在有序号的方格中选出一个画出阴影，使它与图中五个有阴影的正方形一起可以构成正方体表面的展开图，正确的选法是（）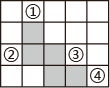

A、只有② B、只有①④ C、只有①②④ D、①②③④都正确

查看试题解析
13. 某电冰箱的进价为1530元，按商品标价的九折出售时，利润率为15%，若设该电冰箱的标价为x元，则可列方程为（）

A、 $90 % x - 1530 = 15 % \times 1530$ B、 $90 % x - 1530 = (1 + 15 %) x$ C、 $1530 \times 90 % = 15 % x$ D、 $x - 1530 \times 90 % = 15 % x$

查看试题解析
14. 观察下列等式：3¹＝3，3²＝9，3³＝27，3⁴＝81，3⁵＝243，3⁶＝729，3⁷＝2187，…，解答问题：3＋3²＋3³＋3⁴＋…＋3²⁰²²的末位数字是（）

A、0 B、1 C、2 D、7

查看试题解析

二、填空题

15. 已知 $a$ 、 $b$ 互为相反数， $c$ 是绝对值最小的数， $d$ 是负整数中最大的数，则 $a + b + c - d =$ ．

查看试题解析
16. 若关于x的方程 $(m - 3) x^{| m - 2 |} - 3 = 0$ 是一元一次方程，则m值是．

查看试题解析
17. 定义新运算：a#b＝3a－2b，则（x＋y）·（x－y）＝．

查看试题解析
18. 如图所示，将一张长方形纸的一角斜折过去，使顶点A落在A′处，BC为折痕．若BD为∠A′BE的平分线，则∠CBD＝．

查看试题解析
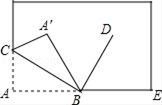19. 已知∠α的补角为105°12'，则它的余角为．

查看试题解析

三、解答题

20. 计算： $- 2^{3} - 5 \times {(- 1)}^{2017} - 9 \div (- 3) \times \frac{1}{3}$

查看试题解析
21. 已知2x^my²与－3xyⁿ是同类项，试计算下面代数式的值：m－(m²n＋3m－4n)＋(2nm²－3n)．

查看试题解析
22. 解方程：

(1)、2（x＋1）＝－5（x－2）

(2)、 $\frac{5 x + 1}{2} - \frac{7 x - 8}{4} = 1$

查看试题解析
23. 如图，已知线段AB＝3cm，延长线段AB到C，使BC＝2AB，延长线段BA到D，使AD：AC＝4：3，点M是BD的中点，求线段BD和AM的长度.

查看试题解析
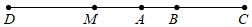24. 已知∠AOB＝40°，OD是∠BOC的平分线．

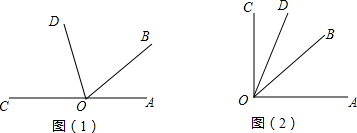(1)、如图1，当∠AOB与∠BOC互补时，求∠COD的度数；

(2)、如图2，当∠AOB与∠BOC互余时，求∠COD的度数．

查看试题解析
25. 某工厂车间有28个工人，生产零件和零件，每人每天可生产A零件18个或B零件12个（每人每天只能生产一种零件），一个A零件配两个B零件，且每天生产的A零件和B零件恰好配套．工厂将零件批发给商场时，每个A零件可获利10元，每个B零件可获利5元．

(1)、求该工厂有多少工人生产A零件？

(2)、因市场需求，该工厂每天要多生产出一部分A零件供商场零售使用，现从生产B零件的工人中调出多少名工人生产A零件，才能使每日生产的零件总获利比调动前多600元？

查看试题解析
26. 如图，直角三角板的直角顶点O在直线AB上，OC，OD是三角板的两条直角边，OE平分∠AOD．

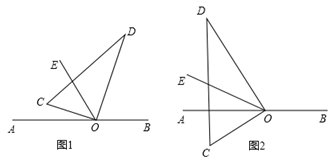(1)、如图1，若∠COE=20°，则∠BOD=；若∠COE=α，则∠BOD=（用含α的代数式表示）；

(2)、将图1中三角板绕O逆时针旋转到图2的位置时，试猜测∠COE与∠BOD之间有怎样的数量关系，并说明理由．

查看试题解析