山东省临沂市河东区2021-2022学年七年级上学期期末考试数学试题
试卷更新日期:2022-12-01 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 根据灯塔实时数据显示,截至12月16日,电影《长津湖》累计票房达到5759000000元,位列中国影史票房榜第四位.将5759000000用科学记数法精确到千万位表示为( )A、 B、 C、 D、3. 已知有理数a,b满足 , 若 , 则为( )A、正数 B、负数 C、零 D、正负不定4. 下列说法正确的是( )A、单项式x3yz4系数是1,次数是7 B、x2y+1是三次二项式 C、单项式的系数是 , 次数是6 D、多项式是四次三项式5. 如图,是正方体的表面展开图,则在“河”、“初”、“数”的三个字的对面依次为( )
河
东
初
中
数
学
A、学、东、中 B、东、学、中 C、东、中、学 D、学、中、东6. 把一副三角尺按如图方式摆放,其中满足一定成立的图形个数共有( ) A、4个 B、3个 C、2个 D、1个7. 平面上有A,B,C三点,经过任意两点画一条直线,可以画出直线的数量为( )A、1条 B、3条 C、1条或3条 D、无数条8. 如图,OA的方向是北偏东15°,OB的方向是西北方向,若∠AOC=∠A0B,则OC的方向是( )
A、4个 B、3个 C、2个 D、1个7. 平面上有A,B,C三点,经过任意两点画一条直线,可以画出直线的数量为( )A、1条 B、3条 C、1条或3条 D、无数条8. 如图,OA的方向是北偏东15°,OB的方向是西北方向,若∠AOC=∠A0B,则OC的方向是( )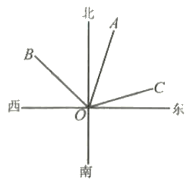 A、北偏东75° B、北偏东60° C、北偏东45° D、北偏东15°9. 在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )A、用两颗钉子就可以把木条固定在墙上; B、当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下; C、把弯曲的公路改直,就能缩短路程; D、在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标.10. 下列方程的变形正确的是( )A、由移项,得 B、由去括号,得 C、由系数化为1,得 D、由去分母,得11. 如图,把一张长方形的纸沿对角线BD折叠,使点C落到点 的位置,若 平分 ,则 的度数是( )
A、北偏东75° B、北偏东60° C、北偏东45° D、北偏东15°9. 在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )A、用两颗钉子就可以把木条固定在墙上; B、当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下; C、把弯曲的公路改直,就能缩短路程; D、在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标.10. 下列方程的变形正确的是( )A、由移项,得 B、由去括号,得 C、由系数化为1,得 D、由去分母,得11. 如图,把一张长方形的纸沿对角线BD折叠,使点C落到点 的位置,若 平分 ,则 的度数是( )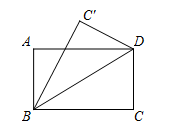 A、15° B、30° C、45° D、60°12. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车:若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、13. 如图所示的几何体是由5个大小相同的小正方体搭成的.从左面看到的平面图形是( )
A、15° B、30° C、45° D、60°12. 《孙子算经》中有一道题,原文是:今有三人共车,二车空:二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车:若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?设共有x人,可列方程( )A、 B、 C、 D、13. 如图所示的几何体是由5个大小相同的小正方体搭成的.从左面看到的平面图形是( )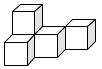 A、
A、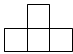 B、
B、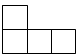 C、
C、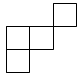 D、
D、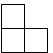 14. 由郑州到北京的某一班次列车,运行途中停靠的车站依次是:鹤壁-安阳-邯郸-邢台-石家庄-保定-北京,那么要为这次列车制作的火车票有( )A、72种 B、56种 C、36种 D、28种
14. 由郑州到北京的某一班次列车,运行途中停靠的车站依次是:鹤壁-安阳-邯郸-邢台-石家庄-保定-北京,那么要为这次列车制作的火车票有( )A、72种 B、56种 C、36种 D、28种二、填空题
-
15. .16. 河东吾悦商场将某品牌的羽绒服在进价的基础上提高60%定价销售,发现销量不好,于是在“元旦”期间将该品牌的羽绒服打六折出售,那么,在“元旦”期间吾悦商场每售出一件这样的羽绒服,将会 . (选填:盈钱、亏钱、不盈不亏钱)17. 某同学走进教室发现黑板前的钟表为8:30,他想知道再过多长时间分针能和时针第一次重合.假设钟表走时准确,请问再过分钟.18. 如图是某月的日历表,在此日历表上可以用一个“十”字圈出5个数(如1,7,8,9,15).照此方法,若圈出的5个数的和为115,则这5个数中的最小数为 .
 19. 《庄子》中“一尺之棰,日取其半,万世不竭”.这句话的意思是:“一尺长的木棍,每天截掉一半,永远也截不完”.根据这句话计算: .
19. 《庄子》中“一尺之棰,日取其半,万世不竭”.这句话的意思是:“一尺长的木棍,每天截掉一半,永远也截不完”.根据这句话计算: .三、解答题
-
20.(1)、计算: .(2)、已知 , 求值: .21. 解下列方程:(1)、 .(2)、 .22. 用8个形状和大小都相同的小长方形,恰好可以拼成如图1所示的大长方形;若用这8个小长方形拼成如图2所示的正方形,则中间留下一个空的小正方形(阴影部分).设小长方形的长和宽分别为a和b().
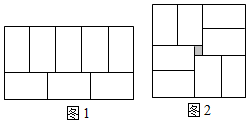 (1)、由图1,可知a,b满足的等量关系是;(2)、若图2中小正方形的边长为3,求小长方形的面积;(3)、用含b的代数式表示图2中小正方形的面积.23. 如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)、由图1,可知a,b满足的等量关系是;(2)、若图2中小正方形的边长为3,求小长方形的面积;(3)、用含b的代数式表示图2中小正方形的面积.23. 如图,以直线AB上一点O为端点作射线OC,使∠AOC=65°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°) (1)、如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE=;(2)、如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;(3)、如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.24. 春节期间,某同学计划租车去旅行,在看过租车公司的方案后,认为有以下两种方案比较适合(注:两种车型的油耗相同):
(1)、如图①,若直角三角板DOE的一边OD放在射线OA上,则∠COE=;(2)、如图②,将直角三角板DOE绕点O顺时针方向转动到某个位置,若OC恰好平分∠AOE,求∠COD的度数;(3)、如图③,将直角三角板DOE绕点O任意转动,如果OD始终在∠AOC的内部,试猜想∠AOD和∠COE有怎样的数量关系?并说明理由.24. 春节期间,某同学计划租车去旅行,在看过租车公司的方案后,认为有以下两种方案比较适合(注:两种车型的油耗相同):日租金(单位:元)
免费行驶里程(单位:千米)
超出部分费用(单位:元/千米)
A型
1200
100
1.5
B型
1500
200
1.2
解决下列问题:
(1)、如果此次旅行的总行程为1800千米,请通过计算说明租用哪种型号的车划算;(2)、设本次旅行行程为x千米,请通过计算说明什么时候选A型车,什么时候选B型车?.25. 甲车和乙车分别从A、B两地同时出发,沿同一路线相向匀速而行.出发后1.5h两车相距80 , 之后再行驶2.5h甲车到达B地,而乙车还差40才能到达A地.求A地和B地相距多少?26. “十·一”黄金周期间,河东龙园在7天假期中每天接待游客的人数变化如下表(正数表示比7天假期平均数多的人数,负数表示比7天假期平均数少的人数)日期
1日
2日
3日
4日
5日
6日
7日
人数变化(千人)
-0.4
+0.6
+0.8
+0.6
-0.8
+0.2
x
(1)、若7天假期中的平均游客人数为2.16千人,则10月7日的游客人数为多少千人?(2)、七天内游客人数最多的一天是哪一天,人数达到多少千人?(3)、若前5天门票每人50元,第5天发现人数开始下降,10月6、7两天在原价的基础上打八折,请求出黄金周期间河东龙园门票总收入是多少万元?