山东省济宁市任城区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列交通标志中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，点O是 $△ A B C$ 内一点， $∠ A = 60 °$ ， $B O$ 、 $C O$ 分别是 $∠ A B C$ 和 $∠ A C B$ 的角平分线，则 $∠ B O C$ 等于（）

A、 $110 °$ B、 $120 °$ C、 $130 °$ D、无法确定

查看试题解析
3. 在3.1415926， $\sqrt{4}$ ， π， $\sqrt{2}$ ， $\sqrt[3]{27}$ ， $\frac{22}{7}$ ， 0.4343343334…（每相邻两个4之间3的个数逐次加1），这些数中无理数的个数为（）

A、4 B、3 C、2 D、1

查看试题解析
4. 如图，已知AB＝DC，AC＝DB，使能得到△ABC≌△DCB，这所依据的是（）

A、SSS B、SSA C、ASA D、SAS

查看试题解析
5. 已知点 $A (m + 2 ， 3)$ 与点 $B (- 4 ， n + 5)$ 关于y轴对称，则 $m + n$ 的值为（）

A、-8 B、0 C、-6 D、-14

查看试题解析
6. 以下列各组数为边长，不能构成直角三角形的是（）

A、3，4，5 B、1，1， $\sqrt{2}$ C、8，12，13 D、 $\sqrt{2}$ , $\sqrt{3}$ , $\sqrt{5}$

查看试题解析
7. 如图所示，已知数轴上的点A，B，C，D分别表示数−2、1、2、3，则表示 $4 - \sqrt{5}$ 的点P落在线段（　　　）

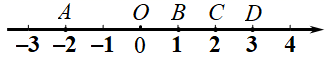A、AO上 B、OB上 C、BC上 D、CD上

查看试题解析
8. 对于一次函数y＝﹣2x+4，下列结论错误的是（）

A、函数的图象不经过第三象限 B、函数的图象与x轴的交点坐标是（2，0） C、函数的图象向下平移4个单位长度得y＝﹣2x的图象 D、若两点A （1，y₁），B （3，y₂）在该函数图象上，则y₁＜y₂

查看试题解析
9. 如图，在平面直角坐标系中，点O为坐标原点，点A的坐标为（-5，12），它关于y轴的对称点为B，则△ABO的周长为（）

A、24 B、34 C、35 D、36

查看试题解析
10. 将一组数 $\sqrt{3}$ ， $\sqrt{6}$ ， 3， $\sqrt{12}$ ， $\sqrt{15}$ ， ……， $\sqrt{90}$ 按下面的方法进行排列：
$\sqrt{3}$ ， $\sqrt{6}$ ， 3， $\sqrt{12}$ ， $\sqrt{15}$ ， $\sqrt{18}$
$\sqrt{21}$ ， $\sqrt{24}$ ， $\sqrt{27}$ ， $\sqrt{30}$ ， $\sqrt{33}$ ， 6
……
若 $\sqrt{12}$ 的位置记为（1，4）， $\sqrt{24}$ 的位置记为（2，2），则这组数中最大的有理数的位置记为（）

A、（5，2） B、（5，3） C、（6，2） D、（6，5）

查看试题解析

二、填空题

11. $\sqrt{9}$ 的平方根是

查看试题解析
12. 如图，点A表示的数为3，过点A作AB⊥OA于点A ，且AB＝2，以O为圆心，OB长为半径作弧，弧与数轴的交点C表示的数是．

查看试题解析
13. 如图，在△ABC中，BH⊥AC交AC于点H，CD平分∠ACB交BH于点D，DH＝3，△BCD的面积为18，则BC的长为．

查看试题解析
14. 如图，在平面直角坐标系中，已知点A（0，4），B（-1，2），C（3，2），直线l经过点A，它将△ABC分成面积相等的两部分，则直线l的表达式为．

查看试题解析
15. 在平面直角坐标系中，一块等腰直角三角板如图放置，其中 $A (2 ， 0)$ ， $B (0 ， 1)$ ，则点 $C$ 的坐标为．

查看试题解析

三、解答题

16. 计算： $\sqrt{36} - \sqrt{(- 3)^{2}} + \sqrt{\frac{1}{4}} - \sqrt[3]{8}$ ．

查看试题解析
17. 如图，在直角坐标平面内，△ABC的三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）．

(1)、填空：AB＝， S_△_ABC＝；

(2)、画出△ABC关于x轴的对称图形△A₁B₁C₁ ，再画出△A₁B₁C₁关于y轴的对称图形△A₂B₂C₂；

(3)、若M是△ABC内一点，且坐标是（a，b），则△A₂B₂C₂中，点M的对应点的坐标为．

查看试题解析
18. 如图，在△ABC中，AB＝AC，AD⊥BC于D，E是AB上的一点，EF∥AD交CA的延长线于F．求证：AF＝AE．

查看试题解析
19. 如图，在△ABC中，AB＝AC，∠ABC的角平分线交AC于点D，过点A作AE∥BC交BD的延长线于点E．若F是DE上的一点，且AD＝AF，求证：BD＝EF．

查看试题解析
20. 我们知道，海拔高度每上升1千米，温度下降6℃．某时刻，某地地面温度为30℃，设高出地面x千米处的温度为y℃．

(1)、请直接写出y与x之间的函数关系式；

(2)、此刻，有一架飞机飞过该地上空，若机舱内仪表显示飞机外面的温度为-36℃．求飞机离地的高度是多少千米？

查看试题解析
21. 小红星期天从家里出发骑车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，买好礼物后又继续骑车去舅舅家，以下是她本次去舅舅家所用的时间与小红离家的距离的关系式示意图．根据图中提供的信息回答下列问题：

(1)、小红家到舅舅家的路程是米，小红在商店停留了分钟；

(2)、在整个去舅舅家的途中哪个时间段小红骑车速度最快？最快的速度是多少米/分？

(3)、本次去舅舅家的行程中，小红一共行驶了多少米？

查看试题解析
22. 如图，直线OA和直线AB的交点坐标为A（8，6），B为直线AB与y轴交点，且OA＝2OB．

(1)、求直线OA和直线AB的函数解析式；

(2)、求△AOB的面积．

查看试题解析
23. 杆秤是我国传统的计重工具，如图，秤钩上所挂的不同重量的物体使得秤砣到秤纽的水平距离不同．称重时，秤钩所挂物重为x（斤）时，秤杆上秤砣到秤纽的水平距离为y（厘米）．如表中为若干次称重时所记录的一些数据，且y是x的一次函数．
x（斤）
0
0.75
1.00
2.25
3.25
y（厘米）
－2
1
2
4
7
注：秤杆上秤砣在秤纽左侧时，水平距离y（厘米）为正，在右侧时为负．

(1)、根据题意，完成表格；

(2)、请求出y与x的关系式；

(3)、当秤杆上秤砣到秤纽的水平距离为15厘米时，秤钩所挂物重是多少斤？

查看试题解析
24. 如图，一次函数y＝- $\frac{3}{4}$ x+3的图象与x轴、y轴分别相交于点A、B，将△AOB沿直线CD对折，使点A和点B重合，直线CD与x轴交于点C，与AB交于点D．

(1)、求A，B两点的坐标；

(2)、求OC的长；

(3)、在x轴上是否存在点P，使△PAB为等腰三角形？如果存在，写出点P的坐标；如果不存在，说明理由．

查看试题解析

x（斤）	0	0.75	1.00		2.25	3.25
y（厘米）	－2	1	2	4	7