山东省济宁市金乡县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣3的绝对值是（）

A、﹣3 B、3 C、- $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 某市决定为全市中小学教室安装空调，今年预计投入资金126000000元，其中数字126000000科学记数法可表示为（）

A、 $12.6 \times 1 0^{7}$ B、 $1.26 \times 1 0^{8}$ C、 $1.26 \times 1 0^{9}$ D、 $0.126 \times 1 0^{10}$

查看试题解析
3. 已知 $∠ α = 60 ° 3 2^{'}$ ，则 $∠ α$ 的余角是（）

A、 $29 ° 2 8^{'}$ B、 $29 ° 6 8^{'}$ C、 $119 ° 2 8^{'}$ D、 $119 ° 6 8^{'}$

查看试题解析
4. 若a-3与1互为相反数，则a的值为（）

A、-3 B、1 C、2 D、0

查看试题解析
5. 小红想设计制作一个圆柱形的礼品盒，下列展开图中设计正确的是（）

A、 B、 C、 D、

查看试题解析
6. 下列说法中，正确的个数有（）
①过两点有且只有一条直线；②连接两点的线段叫做两点间的距离；③两点之间，线段最短；④若∠AOC=2∠BOC，则OB是∠AOC的平分线.

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 小丽同学在做作业时，不小心将方程2（x－3）－■＝x＋1中的一个常数污染了，在询问老师后，老师告诉她方程的解是x＝9，请问这个被污染的常数■是（）

A、4 B、3 C、2 D、1

查看试题解析
8. 一个长方形的周长为 $14 m + 6 n$ ，其中一边的长为 $3 m + 2 n$ ，则另边的长为（）

A、 $4 m + n$ B、 $7 m + 3 n$ C、 $11 m + 4 n$ D、 $8 m + 2 n$

查看试题解析
9. 为配合“我读书，我快乐“读书节活动，某书店推出一种优惠卡，每张卡售价20元，凭卡购书可字受8折优惠．小惠同学到该书店购书，她先买优惠卡，再凭卡付款，结果节省了12元．若此次小惠不买卡直接购书，则她需付款（）

A、160元 B、170元 C、180元 D、200元

查看试题解析
10. 如图，正方形ABCD的边长是2个单位，一只乌龟从A点出发以2个单位/秒的速度顺时针绕正方形运动，另有一只兔子也从A点出发以6个单位/秒的速度逆时针绕正方形运动，1秒后乌龟运动到点D ，兔子也运动到点D ，记为第1次相遇，则第2021次相遇在（）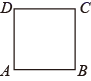

A、点A B、点B C、点C D、点D

查看试题解析

二、填空题

11. 如果收入10元记作+10元，那么支出50元记作元．

查看试题解析
12. 合并同类项： $8 m^{3} n - 5 m^{3} n =$ ．

查看试题解析
13. 若 $2 a - b = 2$ ，则 $6 a - 3 b + 1 =$ ．

查看试题解析
14. 小马在解关于x的一元一次方程 $\frac{3 a - 2 x}{2} = 3 x$ 时，误将- 2x看成了+2x，得到的解为x=6，请你帮小马算一算，方程正确的解为x=.

查看试题解析
15. 我国古代的数学名著《九章算术》中有下列问题：“今有女子善织，日自倍，五日织五尺.问日织几何？”其意思为：今有一女子很会织布，每日加倍增长，5日共织布5尺.问每日各织多少布？根据此问题中的已知条件，可求得该女子第一天织布尺.

查看试题解析

三、解答题

16. 计算：

(1)、 $- 8 + 4 - (- 2) - 3$

(2)、 $- 1^{4} + (- 5) \times (- 8) + (- 2)^{3} \div (- 4)$

查看试题解析
17. 解方程

(1)、 $3 x + 12 = 32 - 2 x$

(2)、 $\frac{3 x + 1}{2} = \frac{5 x - 3}{3} + 1$

查看试题解析
18. 已知：方程 $(m - 2) x^{m + 1} + 3 - m = 11$ 是一元一次方程，求：这个方程的解．

查看试题解析
19. 已知： $A = 2 x^{2} - 3 x y - 2 x - 1$ ， $B = x^{2} - x y + 1$ ．

(1)、求 $A - 2 B$ 的值．

(2)、若 $A - 2 B$ 的值与x的取值无关，求y的值．

查看试题解析
20. 某工厂车间有28个工人，生产零件和零件，每人每天可生产A零件18个或B零件12个（每人每天只能生产一种零件），一个A零件配两个B零件，且每天生产的A零件和B零件恰好配套．工厂将零件批发给商场时，每个A零件可获利10元，每个B零件可获利5元．

(1)、求该工厂有多少工人生产A零件？

(2)、因市场需求，该工厂每天要多生产出一部分A零件供商场零售使用，现从生产B零件的工人中调出多少名工人生产A零件，才能使每日生产的零件总获利比调动前多600元？

查看试题解析
21. 以直线AB上一点O为端点作射线OC，使∠BOC＝40°，将一个直角三角板的直角顶点放在O处，即∠DOE＝90°．

(1)、如图1，若直角三角板DOE的一边OE放在射线OA上，则∠COD＝；

(2)、如图2，将直角三角板DOE绕点O顺时针转动到某个位置，若OE恰好平分∠AOC，则∠COD＝；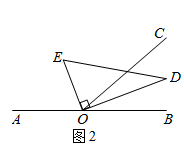

(3)、将直角三角板DOE绕点O顺时针转动（OD与OB重合时为停止）的过程中，恰好有∠COD＝ $\frac{1}{3}$ ∠AOE，求此时∠BOD的度数．

查看试题解析
22. 定义：若有理数a、b满是等式 $a + b - a b = 2$ ，则称a，b是“锥水有数对”记作 $(a ， b)$ ，如：数对 $(2 ， 0)$ ，是“锥水有数对”，其理由：
$∵ 2 + 0 = 2$ ， $2 \times 0 + 2 = 2$
$∴ 2 + 0 = 2 \times 0 + 2$
∴数对 $(2 ， 0)$ ，是“锥水有数对”

(1)、数对 $(4 ， \frac{2}{3})$ 是不是“锥水有数对”？并说明理由．

(2)、若 $(m ， 5)$ 是“锥水有数对”，求m的值．

查看试题解析
23. 【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离AB= $| a - b |$ ，线段AB的中点表示的数为 $\frac{a + b}{2}$ ．如图，数轴上点A表示的数为 $- 2$ ，点B表示的数为8．

(1)、【综合运用】
填空：A，B两点间的距离AB= ，线段AB的中点表示的数为；

(2)、若M为该数轴上的一点，且满足MA+MB=12，求点M所表示的数；

(3)、若点P从点A出发，以每秒1个单位长度的速度沿数轴向终点B匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动，Q到达A点后，再立即以同样的速度返回B点，当点P到达终点后，P、Q两点都停止运动，设运动时间为t秒（ $t > 0$ ）．当t为何值时，P，Q两点间距离为4．

查看试题解析