山东省济南市历城区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-12-01 类型:期末考试
一、单选题
-
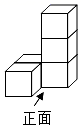
1. ﹣2022的绝对值是( )A、 B、 C、2022 D、﹣20222. 一个由5个相同的正方体组成的立体图形,如图所示,则这个立体图形的左视图是( )
 A、
A、 B、
B、 C、
C、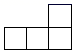 D、
D、 3. 2021年12月9日,某区县初中学生约22600人一起观看了“天宫课堂”第一课,将数字22600用科学记数法表示为( )A、0.226×104 B、2.26×104 C、2.26×103 D、22.6×1044. 要调查下列问题,适合采用抽样调查的是( )A、疫情期间,了解全校师生入校时体温情况 B、检测我国研制的C919大飞机的零件的质量 C、了解一批灯泡的使用寿命 D、了解小明某周每天参加体育运动的时间5. 高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做包含的数学道理是( )A、两点确定一条直线 B、两点之间,线段最短 C、两条直线相交,只有一个交点 D、直线是向两个方向无限延伸的6. 下列计算正确的是( )A、a3+a3=2a6 B、a3⋅a5=a15 C、a6÷a3=a2 D、(-3a3)2=9a67. 若代数式与是同类项,则m的值是( )A、-1 B、0 C、1 D、-28. 过六边形的某一个顶点能画的对角线条数是( )A、6 B、5 C、4 D、39. 若方程3 +6=12的解也是方程6 +3a=24的解,则a的值为( )A、 B、4 C、12 D、210. 如图,将一副三角尺的两个直角顶点O按如图方式叠放在一起,若∠AOC=130°,则∠BOD=( )
3. 2021年12月9日,某区县初中学生约22600人一起观看了“天宫课堂”第一课,将数字22600用科学记数法表示为( )A、0.226×104 B、2.26×104 C、2.26×103 D、22.6×1044. 要调查下列问题,适合采用抽样调查的是( )A、疫情期间,了解全校师生入校时体温情况 B、检测我国研制的C919大飞机的零件的质量 C、了解一批灯泡的使用寿命 D、了解小明某周每天参加体育运动的时间5. 高速公路的建设带动我国经济的快速发展.在高速公路的建设中,通常要从大山中开挖隧道穿过,把道路取直,以缩短路程.这样做包含的数学道理是( )A、两点确定一条直线 B、两点之间,线段最短 C、两条直线相交,只有一个交点 D、直线是向两个方向无限延伸的6. 下列计算正确的是( )A、a3+a3=2a6 B、a3⋅a5=a15 C、a6÷a3=a2 D、(-3a3)2=9a67. 若代数式与是同类项,则m的值是( )A、-1 B、0 C、1 D、-28. 过六边形的某一个顶点能画的对角线条数是( )A、6 B、5 C、4 D、39. 若方程3 +6=12的解也是方程6 +3a=24的解,则a的值为( )A、 B、4 C、12 D、210. 如图,将一副三角尺的两个直角顶点O按如图方式叠放在一起,若∠AOC=130°,则∠BOD=( ) A、45° B、50° C、55° D、60°11. 如图,点C是线段AB的中点,CD=AC,若AD=2cm,则AB=( )
A、45° B、50° C、55° D、60°11. 如图,点C是线段AB的中点,CD=AC,若AD=2cm,则AB=( ) A、3cm B、2.5cm C、4cm D、6cm12. 将正整数按如图所示的规律排列,若用有序数对(a,b)表示第a行,从左至右第b个数,例如(4,3)表示的数是9,则(15,10)表示的数是( )
A、3cm B、2.5cm C、4cm D、6cm12. 将正整数按如图所示的规律排列,若用有序数对(a,b)表示第a行,从左至右第b个数,例如(4,3)表示的数是9,则(15,10)表示的数是( ) A、115 B、114 C、113 D、112
A、115 B、114 C、113 D、112二、填空题
-
13. 计算的结果为 .14. 绵阳冬季某日的最高气温是3℃,最低气温为-1℃,那么当天的温差是℃.15. 一个正方体的平面展开图如图所示,将它折成正方体后“时”字对面的字是 .
 16. 如图,已知点C在点O的东北方向,点D在点O的北偏西20°方向,那么∠COD为度.
16. 如图,已知点C在点O的东北方向,点D在点O的北偏西20°方向,那么∠COD为度. 17. 如图,点E,F分别在长方形ABCD的边AD、CD上,连接BE,将长方形公沿BE对折,点A落在A′处;将∠DEA′对折,点D落在EA′延长线上的D′处,得到折痕EP,若∠BEA′=70°,则∠FED′= .
17. 如图,点E,F分别在长方形ABCD的边AD、CD上,连接BE,将长方形公沿BE对折,点A落在A′处;将∠DEA′对折,点D落在EA′延长线上的D′处,得到折痕EP,若∠BEA′=70°,则∠FED′= .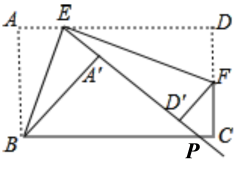 18. 如图,已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2022次相遇在边上.
18. 如图,已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2022次相遇在边上.
三、解答题
-
19. 计算:(1)、(2)、(3)、(4)、20. 先化简,再求值:已知 , 求代数式的值.21. 解方程:(1)、(2)、22. 某学校计划在八年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程.为了解学生对这四门课程的选择情况,学校从八年级全体学生中随机抽取部分学生进行问卷调查.并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出).
 请你根据以上信息解决下列问题:(1)、参加问卷调查的学生人数为 ▲ 名.补全条形统计图(画图并标注相应数据);(2)、在扇形统计图中,选择“陶艺”课程的学生占%;(3)、若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?23. 如图,已知长方形ABCD的宽AB=4,以B为圆心、AB长为半径画弧与边BC交于点E,连接DE,若CE=x,(计算结果保留π)
请你根据以上信息解决下列问题:(1)、参加问卷调查的学生人数为 ▲ 名.补全条形统计图(画图并标注相应数据);(2)、在扇形统计图中,选择“陶艺”课程的学生占%;(3)、若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?23. 如图,已知长方形ABCD的宽AB=4,以B为圆心、AB长为半径画弧与边BC交于点E,连接DE,若CE=x,(计算结果保留π) (1)、BC=(用含x的代数式表示);(2)、用含x的代数式表示图中阴影部分的面积;(3)、当x=4时,求图中阴影部分的面积.24. 某水果销售店用1000元购进甲、乙两种水果共140千克,这两种水果的进价、售价如下表所示:
(1)、BC=(用含x的代数式表示);(2)、用含x的代数式表示图中阴影部分的面积;(3)、当x=4时,求图中阴影部分的面积.24. 某水果销售店用1000元购进甲、乙两种水果共140千克,这两种水果的进价、售价如下表所示:进价(元/千克)
售价(元/千克)
甲种水果
5
8
乙种水果
9
13
(1)、这两种水果各购进多少千克?(2)、若该水果店把这两种水果全部按九折售完,则可获利多少元?
