山东省济南市济阳区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-12-01 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 已知1纳米 , 一个粒子的直径是35纳米,这个粒子的直径用科学记数法表示为( )米.A、 B、 C、 D、3. 若 , 则的补角的度数是( )A、40° B、50° C、130° D、140°4. 如图, , 平分 , , 则的度数为( )
 A、30° B、35° C、40° D、45°5. 将一根长为 的铁丝制作成一个长方形,则这个长方形的长 与宽 之间的关系式为( )A、 B、 C、 D、6. 某科研小组在网上获取了声音在空气中传播的速度y与空气温度x关系的一些数据
A、30° B、35° C、40° D、45°5. 将一根长为 的铁丝制作成一个长方形,则这个长方形的长 与宽 之间的关系式为( )A、 B、 C、 D、6. 某科研小组在网上获取了声音在空气中传播的速度y与空气温度x关系的一些数据温度x(/C)
- 20
- 10
0
10
20
30
声速y(/m/s)
318
324
330
336
342
348
下列说法错误的是( )
A、在这个变化中,自变量是温度,因变量是声速 B、温度越高,声速越快 C、当空气温度为20℃时,声音5s可以传播1740m D、温度每升高10℃,声速提高6m/s.7. 下列哪组长度的三条线段能组成三角形?( )A、1cm、2cm、4cm B、3cm、4cm、7cm C、2cm、2cm、1cm D、5cm、3cm、2cm8. 下列图片中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 9. 一个不透明的袋中装有 7个只有颜色,不同的球,其中3个红球,2个蓝球和2个黄球.从袋中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、10. 分别写有数字-1,-2,1,3,4的五张卡片,除数字外其他均相同,将它们背面朝上,从中任抽一张,抽到负数的概率是( )A、 B、 C、 D、11. (2+1)(22+1)(24+1)…(216+1)的结果为( )A、232-1 B、232+1 C、232 D、21612. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第2022个三角形中以A2021为顶点的底角度数是( )
9. 一个不透明的袋中装有 7个只有颜色,不同的球,其中3个红球,2个蓝球和2个黄球.从袋中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、10. 分别写有数字-1,-2,1,3,4的五张卡片,除数字外其他均相同,将它们背面朝上,从中任抽一张,抽到负数的概率是( )A、 B、 C、 D、11. (2+1)(22+1)(24+1)…(216+1)的结果为( )A、232-1 B、232+1 C、232 D、21612. 如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第2022个三角形中以A2021为顶点的底角度数是( )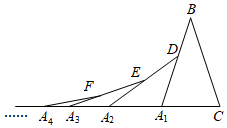 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 计算 .14. 从编号为1到10的10张卡片中任取1张,所得编号是4的倍数的概率为 .15. 小亮早晨从家骑车到学校,先上坡后下坡,所行路程与时间的关系如图所示,若返回时上坡、下坡的速度仍与去时上坡、下坡的速度分别相同,则小明从学校骑车回家用的时间是 .
 16. 如图,在△ABC中,点D、E分别为边AC、BC上的点,且AD=DE,AB=BE,∠A=70°,则∠CED=度.
16. 如图,在△ABC中,点D、E分别为边AC、BC上的点,且AD=DE,AB=BE,∠A=70°,则∠CED=度. 17. 如图,把一张三角形纸片(△ABC)进行折叠,使点A落在BC上的点F处,折痕为DE,点D,点E分别在AB和AC上,DE∥BC,若∠B=70°,则∠BDF的度数为 .
17. 如图,把一张三角形纸片(△ABC)进行折叠,使点A落在BC上的点F处,折痕为DE,点D,点E分别在AB和AC上,DE∥BC,若∠B=70°,则∠BDF的度数为 . 18. 如图,大正方形ABCD的边长为 , 小正方形CEFG的边长为 , 则阴影部分的面积是 ;
18. 如图,大正方形ABCD的边长为 , 小正方形CEFG的边长为 , 则阴影部分的面积是 ;
三、解答题
-
19.(1)、计算:(2)、化简:(3)、先化简,再求值: , 其中 .(4)、请用简便方法计算:899×901+1(5)、请用简便方法计算:1.372+2×1.37×8.63+8.632;20. 如图,已知直线AB∥CD,∠B=50°,∠BEC=25°,EC平分∠BEF.
 (1)、请说明AB∥EF的理由;(2)、求∠DCE的度数.21. 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)、请说明AB∥EF的理由;(2)、求∠DCE的度数.21. 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题: (1)、求该团去景点时的平均速度是多少?(2)、该团在旅游景点游玩了多少小时?(3)、求返回到宾馆的时刻是几时几分?22. 商店在出售某商品时,在进价的基础上增加一定的利润,其质量x与售价y之间的关系如下表所示:
(1)、求该团去景点时的平均速度是多少?(2)、该团在旅游景点游玩了多少小时?(3)、求返回到宾馆的时刻是几时几分?22. 商店在出售某商品时,在进价的基础上增加一定的利润,其质量x与售价y之间的关系如下表所示:质量x/千克
1
2
3
4
…
售价y/元
8+0.4
16+0.8
24+1.2
32+1.6
…
(1)、请根据表中提供的信息,写出y与x的关系式;(2)、求x=2.5时,y的值;(3)、当x取何值时,y=126?23. 一个不透明的口袋中放有290个涂有红、黑、白三种颜色的质地相同的球.已知红球的个数比黑球的2倍多40个,从袋中任取一个球是黑球的概率是 .(1)、袋中黑球的个数为个,袋中红球的个数是个;(2)、求从袋中任取一个球是白球的概率.24. 如图,在△ABC中,O为BC中点,BDAC,直线OD交AC于点E. (1)、求证:△BDO≌△CEO;(2)、若AC=6,BD=4,求AE的长.25. 如图,在正方形网格中,点A、B、C、M、N都在格点上.
(1)、求证:△BDO≌△CEO;(2)、若AC=6,BD=4,求AE的长.25. 如图,在正方形网格中,点A、B、C、M、N都在格点上.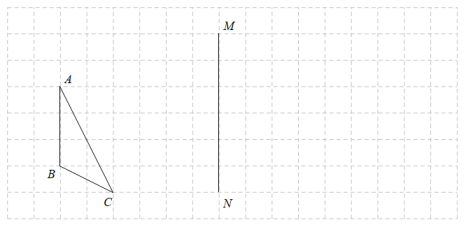 (1)、作关于直线MN对称的图形 .(2)、若网格中最小正方形的边长为2,求的面积.(3)、点P在直线MN上,当周长最小时,P点在什么位置,在图中标出P点.26. 如图,端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定顾客每购买200元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准红、黄、绿的区域,顾客就可以分别获得50元、20元、10元的奖金,对准无色区域则无奖金(转盘等分成16份).
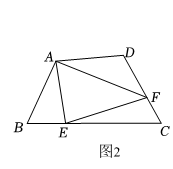
(1)、作关于直线MN对称的图形 .(2)、若网格中最小正方形的边长为2,求的面积.(3)、点P在直线MN上,当周长最小时,P点在什么位置,在图中标出P点.26. 如图,端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定顾客每购买200元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针上对准红、黄、绿的区域,顾客就可以分别获得50元、20元、10元的奖金,对准无色区域则无奖金(转盘等分成16份). (1)、小明购物180元,他获得奖金的概率是多少?(2)、小德购物210元,那么获得奖金的概率是多少?(3)、现商场想调整获得10元奖金的概率为 , 其他金额的获奖率不变,则需要将多少个无色区域涂上绿色?27. 初步探索:如图:在四边形中, , , 、分别是、上的点,且 , 探究图中、、之间的数量关系.
(1)、小明购物180元,他获得奖金的概率是多少?(2)、小德购物210元,那么获得奖金的概率是多少?(3)、现商场想调整获得10元奖金的概率为 , 其他金额的获奖率不变,则需要将多少个无色区域涂上绿色?27. 初步探索:如图:在四边形中, , , 、分别是、上的点,且 , 探究图中、、之间的数量关系. (1)、小明同学探究此问题的方法是:延长到点 , 使 . 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是;(2)、如图2,若在四边形中, , , 、分别是、上的点,且 , 上述结论是否仍然成立,并说明理由;
(1)、小明同学探究此问题的方法是:延长到点 , 使 . 连接 , 先证明 , 再证明 , 可得出结论,他的结论应是;(2)、如图2,若在四边形中, , , 、分别是、上的点,且 , 上述结论是否仍然成立,并说明理由;