山东省东营市河口区2021-2022学年七年级上学期期末数学试卷

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. 第24届冬季奥林匹克运动会，将于2022年02月04日～2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在实数 $\sqrt[3]{- 9}$ ， 3.1415926，0.123123123…， $\frac{π}{2}$ ， $\sqrt{4}$ ， 0.2020020002…（相邻两个2中间一次多1个0）中，无理数有（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 对于一次函数y＝﹣2x+4，下列结论错误的是（）

A、函数的图象不经过第三象限 B、函数的图象与x轴的交点坐标是(2，0) C、函数的图象向下平移4个单位长度得y＝﹣2x的图象 D、若两点A(x₁ ， y₁)，B(x₂ ， y₂)在该函数图象上，且x₁＜x₂ ，则y₁＜y₂

查看试题解析
4. 估算9- $\sqrt{10}$ 的值，下列结论正确的是（）

A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间

查看试题解析
5. 如图，AB⊥BC，EC⊥BC，AD⊥DE，AD=DE，AB=3，BC=8，则CE长为（）

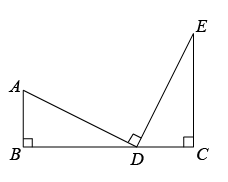A、4 B、5 C、8 D、10

查看试题解析
6. 我国古代数学著作《九章算术》记载了一道有趣的问题．原文是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐．问水深、葭长各几何．译为：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面，水的深度与这根芦苇的长度分别是多少？设芦苇的长度是x尺．根据题意，可列方程为（）

A、（x-1）²+5²＝x² B、x²+10²＝（x+1）² C、（x-1）²+10²＝x² D、x²+5²＝（x+1）²

查看试题解析
7. 如图所示，在△ABC中，已知点D，E，F分别是BC，AD，CE的中点，S_△_ABC=4平方厘米，则S_△_BEF的值为（）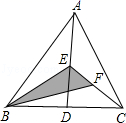

A、2平方厘米 B、1平方厘米 C、 $\frac{1}{2}$ 平方厘米 D、 $\frac{1}{4}$ 平方厘米

查看试题解析
8. 如图，在四边形ABCD中，AD∥BC，∠C=90°，△BCD与△BC′D关于直线BD轴对称，BC=6，CD=3，点C与点C′对应，BC′交AD于点E，则线段DE的长为（）

A、3 B、 $\frac{15}{4}$ C、5 D、 $\frac{15}{2}$

查看试题解析
9. 已知正比例函数y＝kx（k≠0）的函数值y随x的增大而减小，则一次函数y＝﹣kx+k的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
10. 如图，已知AB=AC，∠A=36°，AB的垂直平分线MD交AC于点D，AB于M，以下结论：①△BCD是等腰三角形；②射线BD是△ACB的角平分线；③△BCD的周长C_△BCD=AC+BC；④△ADM≌△BCD．正确的有（）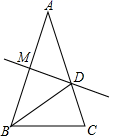

A、①②③ B、①② C、①③ D、③④

查看试题解析

二、填空题

11. $\sqrt{9}$ 的平方根是

查看试题解析
12. 请仔细观察用直尺和圆规作一个 $∠ A^{'} O^{'} B^{'}$ 等于已知角 $∠ A O B$ 的示意图，请你根据所学的三角形全等的有关知识，说明画出 $∠ A^{'} O^{'} B^{'} = ∠ A O B$ 的依据是（填简写）

查看试题解析
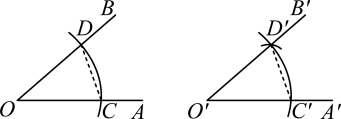13. 已知点P（a，b）在一次函数y＝2x﹣1的图象上，则4a﹣2b+1＝.

查看试题解析
14. 在平面直角坐标系中，线段AB平行于x轴，且AB＝4．若点A的坐标为（﹣1，2），点B的坐标为（a，b），则a+b＝．

查看试题解析
15. 如图，Rt $△$ ABC的斜边AB的垂直平分线MN与AC交于点M，∠A=15°，BM=4，则 $△$ AMB的面积为．

查看试题解析
16. 如图，圆柱形容器的高为0.9m，底面周长为1.2m，在容器内壁离容器底部0.3m处的点B处有一蚊子．此时，一只壁虎正好在容器外壁，离容器上沿0.2m与蚊子相对的点A处，则壁虎捕捉蚊子的最短距离为 m．

查看试题解析
17. 如图， $l_{1}$ 表示某机床公司一天的销售收入与机床销售量的关系， $l_{2}$ 表示该公司一天的销售成本与机床销售量的关系.有以下四个结论：① $l_{1}$ 对应的函数表达式是y=x；② $l_{2}$ 对应的函数表达式是y=x+1；③当销售量为2件时，销售收入等于销售成本；④利润与销售量之间的函数表达式是w=0.5x-1.其中正确的结论为（请把所有正确的序号填写在横线上）.

查看试题解析
18. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2）…按这样的运动规律经过第2021次运动后，动点P的坐标是．

查看试题解析

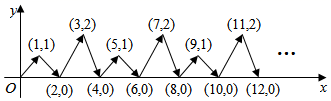
三、解答题

19. 计算：

(1)、（ $\sqrt{2}$ ）²+ $\sqrt{(- 3)^{2}}$ -（ $\sqrt[3]{3}$ ）³+ $\sqrt[3]{- 125}$ ；

(2)、（2021-π）⁰- $\sqrt{25}$ +（- $\frac{1}{3}$ ）^-²- $\sqrt[3]{- 27}$ -| $\sqrt{5}$ -3|．

查看试题解析
20. $△ A B C$ 在方格纸（小正方形的边长为1）中的位置如图所示．

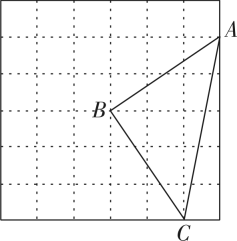(1)、判断 $△ A B C$ 的形状，并说明理由；

(2)、建立平面直角坐标系，使C点的坐标是（1，-3），并写出点A，B的坐标；

(3)、画出 $△ A B C$ 关于y轴对称的图形 $△ A^{'} B^{'} C^{'}$ ．

查看试题解析
21. 如图，已知∠A=90°，∠ADE=120°，BD平分∠ADE，AD=DE．

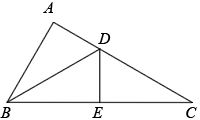(1)、 $△ B A D$ 与 $△ B E D$ 全等吗？请说明理由；

(2)、若DE=2，试求AC的长．

查看试题解析
22. 某中学在校园一角开辟了一块四边形的“试验田”，把课堂的“死教材”转换为生动的“活景观”，学生们在课堂上学习理论之余，还可以到“试验田”实际操练，对生物的发展规律有了更为直观的认识．如图，四边形 $A B C D$ 是规划好的“试验田”，经过测量得知： $∠ B = 90 °$ ， $A B = 24 m$ ， $B C = 7 m$ ， $C D = 15 m$ ， $A D = 20 m$ ．求四边形 $A B C D$ 的面积．

查看试题解析
23. 随着春节临近，某儿童游乐场推出了甲、乙两种消费卡，设消费次数为x时，所需费用为y元，且y与x的函数关系如图所示. 根据图中信息，解答下列问题；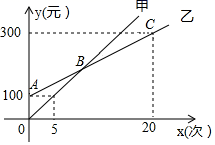

(1)、分别求出选择这两种卡消费时，y关于x的函数表达式.

(2)、求出B点坐标.

(3)、洋洋爸爸准备 $240$ 元钱用于洋洋在该游乐场消费，请问选择哪种消费卡划算？

查看试题解析
24. 有一辆装满货物的卡车，高2.5米，宽1.6米，要开进如图所示的上边是半圆，下边是长方形的桥洞，已知半圆的直径为2米，长方形的另一条边长是2.3米.

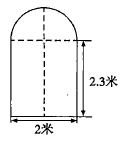(1)、这辆卡车能否通过此桥洞？试说明你的理由.

(2)、为了适应车流量的增加，想把桥洞改为双行道，并且要使宽1.2米，高为2.8米的卡车能安全通过，那么此桥洞的宽至少应增加到多少米？

查看试题解析
25. 数学兴趣小组在活动时，老师提出了这样一个问题：
如图1，在 $△ A B C$ 中， $A B = 6$ ， $A C = 10$ ， D是BC的中点，求BC边上的中线AD的取值范围．

(1)、【阅读理解】
小明在组内经过合作交流，得到了如下的解决方法：

如图1，延长AD到E点，使 $D E = A D$ ，连接BE．根据可以判定 $△ A D C ≌$ ，得出 $A C =$ ．

这样就能把线段AB、AC、 $2 A D$ 集中在 $△ A B E$ 中．利用三角形三边的关系，即可得出中线AD的取值范围是．

(2)、【方法感悟】
当条件中出现“中点”、“中线”等条件时，可以考虑做“辅助线”——把中线延长一倍，构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中，这种做辅助线的方法称为“中线加倍”法．

【问题解决】

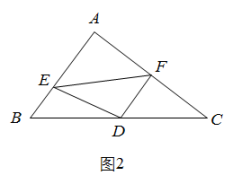
如图2，在 $△ A B C$ 中， $∠ A = 9 0^{∘}$ ， D是BC边的中点， $∠ E D F = 9 0^{∘}$ ， DE交AB于点E，DF交AC于点F，连接EF，求证： $B E^{2} + C F^{2} = E F^{2}$ ．

(3)、【问题拓展】
如图3， $△ A B C$ 中， $∠ B = 9 0^{∘}$ ， $A B = 3$ ， AD是 $△ A B C$ 的中线， $C E ⊥ B C$ ， $C E = 5$ ，且 $∠ A D E = 9 0^{∘}$ ．直接写出AE的长＝．

查看试题解析