山东省东营市广饶县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. 2022年冬奥会将在北京举行，以下历届冬奥会会徽是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 第24届冬季奥林匹克运动会将于2022年由北京市和张家口市联合举行．以下能够准确表示张家口市地理位置的是（）

A、离北京市200千米 B、在河北省 C、在宁德市北方 D、东经114.8°，北纬40.8°

查看试题解析
3. 下列说法正确的是（）

A、大于0小于 $π$ 的整数是1和2 B、算术平方根等于它本身的数只有1 C、立方根等于它本身的数只有0或1 D、数轴上表示 $\sqrt{10}$ 的点在3和4之间

查看试题解析
4. 已知等腰三角形的一边长为9，另一边长为4，则它周长是（）

A、13 B、22 C、17 D、17或22

查看试题解析
5. 对于一次函数 $y = - 2 x + 1$ 的相关性质，下列描述错误的是（）

A、函数图象经过第一、二、四象限 B、图象与y轴的交点坐标为 $(1 ， 0)$ C、y随x的增大而减小 D、图象与坐标轴调成三角形的面积为 $\frac{1}{4}$

查看试题解析
6. 如图，∠ACB＞90°，AD⊥BC，BE⊥AC，CF⊥AB，垂足分别为点D、点E、点F，△ABC中AC边上的高是（）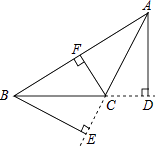

A、CF B、BE C、AD D、CD

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， C D ⊥ A B$ ，垂足为D，下列结论中，不一定成立的是（）

A、 $∠ A$ 与 $∠ 1$ 互余 B、 $∠ B$ 与 $∠ 2$ 互余 C、 $∠ A = ∠ 2$ D、 $∠ 1 = ∠ 2$

查看试题解析
8. 如图，∠AOB内一点P，P₁ ， P₂分别是P关于OA、OB的对称点，P₁P₂交OA于点M，交OB于点N．若△PMN的周长是5cm，则P₁P₂的长为（）

A、6cm B、5cm C、4cm D、3cm

查看试题解析
9. 我图古代数学著作《九章算术》中有这样一个问题：今有方池一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深几何？（注：丈、尺是长度单位，1丈=10尺）意思为：如图，有一个边长为1丈的正方形水池，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的岸边，它的顶端恰好碰到池边的水面．则这根芦苇的长度是（）

A、5尺 B、10尺 C、12尺 D、13尺

查看试题解析
10. 如图①是某公共汽车线路收支差额y（票价总收入减去运营成本）与乘客量x的函数图象，目前这条线路亏损，为了扭亏，有关部门举行提高票价的听证会，乘客代表认为：公交公司应降低运营成本，实现扭亏，公交公司认为：运营成本难以下降，提高票价才能扭亏根据这两种意见，把图①分别改画成图②和图③．则下列判断不合理的是（）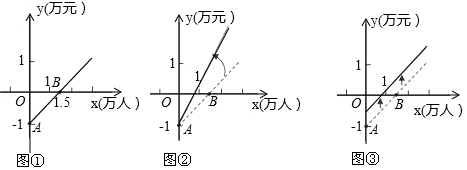

A、图①中点A的实际意义是公交公司运营后亏损1万元 B、图①中点B的实际意义是乘客量为1.5万时公交公司收支平衡 C、图②能反映公交公司意见 D、图③能反映乘客意见

查看试题解析

二、填空题

11. 一个正方体形状得木箱容积是 $8 m^{3}$ ，则此木箱的边长是m．

查看试题解析
12. 已知|m+5|+ $\sqrt{n - 3}$ ＝0，点P（m，n）关于x轴的对称点的坐标是．

查看试题解析
13. 已知x是16的算术平方根，y是9的平方根，则 $x^{2} + y^{2} - x - 1$ 的值为．

查看试题解析
14. 若函数 $y = (k - 2) x^{| k - 1 |} + 1$ 是表示一次函数，则k等于．

查看试题解析
15. 如图，在 $△ A B C$ 中，已知AD是 $∠ A$ 平分线， $D E ⊥ A C$ 于点E， $A C = 4 ， A B = 6 ， S_{△ A B C} = 10$ ，则点D到AB的最短距离是．

查看试题解析
16. 如图，为做好疫情防控，小航同学在超市帮妈妈买回一袋纸杯，他把纸杯整齐地叠放在一起，请根据图中信息，如果把这袋60个纸杯整齐叠放在一起时，它的高度为 $c m$ ．

查看试题解析
17. 如图，BE交AC于点M，交CF于点D，AB交CF于点N， $∠ E = ∠ F = 90 ° ， ∠ B = ∠ C ， A E = A F$ ，给出的下列五个结论中正确结论的序号为．
① $∠ 1 = ∠ 2$ ；② $B E = C F$ ；③ $△ C A N ≅ △ B A M$ ；④ $C D = D N$ ；⑤ $△ A F N ≌ △ A E M$ ．

查看试题解析
18. 观察下列各组勾股数
（ 1 ）3，4，5
（ 2 ）5，12，13；
（ 3 ）7，24，25：
（ 4 ）9，40，41
照此规律，将第n组勾股数按从小到大的顺序排列，排在中间的数，用含n的代数式可表示为．

查看试题解析

三、解答题

19. 计算

(1)、 $\sqrt{144} - {(2022 - π)}^{0} + \sqrt{{(- 3)}^{2}}$ ；

(2)、 $\sqrt{900} - \sqrt[3]{27} + (\sqrt[3]{9})^{3}$ ；

(3)、 $x^{2} = \frac{25}{81}$ ；

(4)、 $\sqrt{\frac{25}{9}} + \sqrt[3]{- \frac{125}{27}} + | \sqrt{2} - 2 |$

查看试题解析
20. 如图，要测量水池中一朵荷花E距岸边A和岸边D的距离．作法如下：
①任作线段AB，取中点O；
②连接DO并延长至点C，使 $C O = D O$ ；
③连接BC；
④用仪器测得E、O在一条直线上，且直线EO交CB于点F，要测量AE、DE，则只需测量BF、DF即可，为什么？

查看试题解析
21. 2021年10月10日是辛亥革命110周年纪念日．为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神，社区开展了系列纪念活动．如图，有一块四边形空地，社区计划将其布置成展区，陈列有关辛亥革命的历史图片．现测得 $A B = A D = 26 m$ ， $B C = 16 m$ ， $C D = 12 m$ ，且 $B D = 20 m$ ．

(1)、试说明 $∠ B C D = 90 °$ ；

(2)、求四边形展区（阴影部分）的面积．

查看试题解析
22. 尺规作图：（不要求写作法，只保留作图痕迹）
第24届冬奥会2022年2月4日在北京市和张家口市联合举行．现有两个比赛场地A、B位于两条公路OC、OD之间的地带，现要建一座物流中转站P，若要求中转站P到两条公路OC、OD的距离相等，且到两个比赛场地A和B的距离相等，请用尺规作出点P的位置．

查看试题解析
23. 如图，在平面直角坐标系中， $△ A B C$ 顶点的坐标分别是 $A (- 1.3) ， B (- 5.1) ， C (- 2 ， - 2)$ ．
（ 1 ）画出 $△ A B C$ 关于y轴对称的 $△ A^{'} B^{'} C^{'}$ ，并写出 $△ A^{'} B^{'} C^{'}$ 各顶点的坐标；
（ 2 ）求出 $△ A B C$ 的面积，
（ 3 ）在y轴上作点P，使得 $P A + P B$ 的值最小（不要求写作法，只保留作图痕迹）．

查看试题解析
24. 如图， $l_{1}$ 反映了某公司产品的销售收入与销售量的关系， $l_{2}$ 反映了该公司的销售成本与销售量的关系，观察图象，回答下列问题．

(1)、当销售量为6吨时，销售收入为元，销售成本为元；利润（收入-成本）为元；

(2)、当销售量每增加1吨，销售收入增加元；产品未销售时，销售成本为元；

(3)、求利润w（元）（销售收入-销售成本）与销售量x（吨）之间的函数关系式．

查看试题解析
25. 在△ABC中，∠BAC＝90°，AC＝AB，点D为直线BC上的一动点，以AD为边作△ADE（顶点A、D、E按逆时针方向排列），且∠DAE＝90°，AD＝AE，连接CE.

(1)、如图1，若点D在BC边上（点D与B、C不重合），求∠BCE的度数.

(2)、如图2，若点D在CB的延长线上，若DB＝5，BC＝7，求△ADE的面积．

查看试题解析
26. 如图1，点B在线段CE上， $A C ⊥ C E ， F E ⊥ C E$ ，垂足分别为C、E，且 $A C = B E ， B C = E F$ ，连接AB、BF、AF，解答下列问题：

(1)、判断 $△ A B F$ 的形状，并说明理由．

(2)、梯形是只有一组对边平行的四边形，平行的两边叫做梯形的底边，较短的一条底边叫上底，较长的一条底边叫下底，另外两边叫腰，夹在两底之间的垂线段叫梯形的高．梯形的面积公式为： $\frac{1}{2} \times （上底 + 下底） \times 高$ ．若 $A B = c ， A C = b ， B C = a$ ，且四边形ACEF为梯形．请通过求梯形ACEF面积不同的计算方法验证：在 $Rt △ A B C$ 中，两直角边a、b和斜边c满足 $a^{2} + b^{2} = c^{2}$ ．

(3)、利用（2）中验证的结论解答下列问题：
①若 $Rt △ A B C$ 两条直角边长分别为3、4，则斜边的长为；

②如图2，有两棵树，一棵高12米，另一棵高5米，两棵树树梢相距8米，一只鸟从矮树的树梢飞到另一棵数的最短距离是米．

查看试题解析