山东省滨州市无棣县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $- 2022 \times □ = 1$ ，那么“□”内应填的数是（）

A、 $\frac{1}{2022}$ B、2022 C、 $- \frac{1}{2022}$ D、 $- 2022$

查看试题解析
2. 小马虎在下面的计算中，只做对了一道题，他做对的题目是（）

A、 $5 a - a = 4 a^{2}$ B、 $9 y - 6 y = 3$ C、 $5 x^{2} y - 8 y x^{2} = - 3 x^{2} y$ D、 $3 a + 3 b = 6 a b$

查看试题解析
3. 用四舍五入法将有理数3.14159精确到万分位的结果是（）

A、3.1410 B、3.1420 C、3.1415 D、3.1416

查看试题解析
4. 下列四个生活、生产现象：①用两枚钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③体育课上，老师测量某同学的跳远成绩；④把弯曲的公路改直，就能缩短路程．其中可用基本事实“两点确定一条直线”来解释的现象有（）

A、①②③ B、①② C、②④ D、①③④

查看试题解析
5. 如图，数轴上点A对应的数是 $\frac{3}{2}$ ，将点A沿数轴向右移动2个单位至点B，则点B对应的数是（）

A、 $\frac{7}{2}$ B、 $- 3$ C、 $\frac{9}{2}$ D、 $- \frac{1}{2}$

查看试题解析
6. 计算 $- \frac{2}{5} - (- \frac{3}{5})$ 的结果为（）

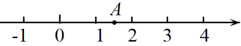A、 $- 1$ B、1 C、 $- \frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
7. 《算法统宗》是中国古代数学名著，作者是我国明代数学家程大位．在《算法统宗》中记载：“以绳测井，若将绳三折测之，绳多4尺，若将绳四折测之，绳多1尺，绳长井深各几何？”
译文：“用绳子测水井深度，如果将绳子折成三等份，井外余绳4尺；如果将绳子折成四等份，井外余绳1尺．问绳长、井深各是多少尺？”

设井深为x尺，根据题意列方程，正确的是（）

A、3（x+4）=4（x+1） B、3x+4=4x+1 C、3（x﹣4）=4（x﹣1） D、 $\frac{x}{3} - 4 = \frac{x}{4} - 1$

查看试题解析
8. 如图，下列说法正确的是（）

A、图中有两条线段 B、图中共有6条射线 C、射线 $A B$ 与射线 $B C$ 是同一射线 D、直线 $A C$ 与直线 $B C$ 不同

查看试题解析
9. 已知 $4 x^{4} y^{m - 2}$ 和 $- x^{2 n - 2} y^{2}$ 是同类项，则式子 $(m - n)^{2022}$ 的值是（）

A、1 B、 $- 1$ C、0 D、2022

查看试题解析
10. 历史上数学家欧拉最先把关于x的多项式用记号 $f (x)$ 来表示，把x等于某数a时的多项式的值用 $f (a)$ 来表示．例如，对于多项式 $f (x) = m x^{3} + n x - 4$ ，当 $x = 3$ 时，多项式的值为 $f (3) = 27 m + 3 n - 4$ ，若 $f (3) = 8$ ，则 $f (- 3)$ 的值为（）

A、 $- 8$ B、8 C、16 D、 $- 16$

查看试题解析
11. 如图，学校（记作A）在爱棣家（记作B）西偏南 $62 °$ 的方向上，且与爱棣家的距离是 $4 k m$ ，若 $∠ A B C = 90 °$ ，且 $A B = 2 B C$ ，则超市（记作C）在爱棣家的（）

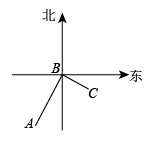A、南偏东 $62 °$ 的方向上，相距 $4 k m$ B、南偏东 $62 °$ 的方向上，相距 $2 k m$ C、南偏东 $28 °$ 的方向上，相距 $2 k m$ D、东偏南 $62 °$ 的方向上，相距 $2 k m$

查看试题解析
12. 如图，线段AB的长为m，点C为AB上一动点（不与A，B重合），D为AC中点，E为BC中点，随着点C的运动，线段DE的长度（）

A、随之变化 B、不改变，且为 $\frac{2}{3} m$ C、不改变，且为 $\frac{3}{5} m$ D、不改变，且为 $\frac{1}{2} m$

查看试题解析

二、填空题

13. 用“>”或“<”符号填空： $- \frac{1}{4}$ $- \frac{1}{5}$ ．

查看试题解析

14. 在一次综合复习检测中爱国同学的填空题的答卷情况如图所示，他的得分应是分．

姓名：爱国得分

填空题（每小题2分，共10分）

⑴单项式 $- \frac{2 x^{2} y}{3}$ 的系数是（ $- 2$ ）；

⑵相反数等于本身的数是（0）；

⑶如果上升 $8 ℃$ 记作 $+ 8 ℃$ ，那么下降 $4 ℃$ 记（ $- 4$ ） $℃$ ；

⑷ $∠ a = 40.4 ° ， ∠ B = 40 ° 4^{'}$ ，则 $∠ a$ （=） $∠ B$ ；（填：>、<或=）

⑸去括号： $x - (y - z) =$ （ $x - y + z$ ）．

查看试题解析

15. 某种商品每件的进价为200元，标价为300元．为了拓展销路，商店准备打折销售．若使利润率为20%，则商店应打折．

查看试题解析
16. 如图是一个正方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数，则 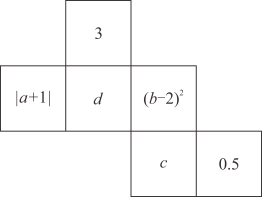$a + b - c^{2} + 2 d$ 的值是．

查看试题解析
17. 下列图形是由一些小正方形和实心圆按一定规律排列而成的，如图所示，按此规律排列下去，第2022个图形中有个实心圆．

查看试题解析
18. 把一副三角尺按如图所示拼在一起，其中 $B$ ， $C$ ， $D$ 三点在同一直线上， $C M$ 平分 $∠ A C B$ ， $C N$ 平分 $∠ D C E$ ，则 $∠ M C N =$ $°$ .

查看试题解析

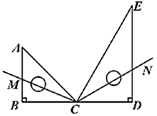
三、解答题

19.

(1)、计算： $- 2^{3} \div \frac{4}{9} \times {(- \frac{2}{3})}^{2} + (- 1)^{100} \times 5$ ；

(2)、先化简再求值： $\frac{1}{2} a - 2 (a - \frac{1}{3} b^{2}) + (- \frac{3}{2} a + \frac{1}{3} b^{2})$ ，其中 $a = - 2 ， b = \frac{2}{3}$ ．

查看试题解析

20. 学习了一元一次方程的解法后，老师布置了这样一道计算题

\frac{3 x - 1}{4} - 1 = \frac{5 x - 7}{6}

，甲、乙两位同学的解答过程分别如下：

甲同学：

解方程 $\frac{3 x - 1}{4} - 1 = \frac{5 x - 7}{6}$ ．

解： $\frac{3 x - 1}{4} \times 12 - 1 \times 12 = \frac{5 x - 7}{6} \times 12$ 第①步

$3 (3 x - 1) - 12 = 2 (5 x - 7)$ 第②步

$3 x - 1 - 12 = 10 x - 7$ 第③步

$3 x - 10 x = - 7 + 1 + 12$ 第④步

$- 7 x = 6$ 第⑤步

$x = - \frac{6}{7}$ ．第⑥步

乙同学：

解方程 $\frac{3 x - 1}{4} - 1 = \frac{5 x - 7}{6}$ ．

解： $\frac{3 x - 1}{4} \times 12 - 1 = \frac{5 x - 7}{6} \times 12$ 第①步

$3 (3 x - 1) - 1 = 2 (5 x - 7)$ 第②步

$3 x - 3 - 1 = 10 x - 14$ 第③步

$3 x - 10 x = - 14 + 1 + 3$ 第④步

$- 7 x = - 10$ 第⑤步

$x = - \frac{10}{7}$ ．第⑥步

老师发现这两位同学的解答过程都有错误，请回答以下问题：

(1)、甲同学的解答过程从第步开始出现错误（填序号）；

(2)、乙同学的解答过程从第步开始出现错误（填序号）；错误的原因是．

(3)、请写出正确的解答过程．

查看试题解析

21.

(1)、已知 $x = - 1$ 是关于x的方程 $2 k - x - k (x + 4) = - 2$ 的解，求k的值；

(2)、在（1）的条件下，已知线段 $A B = 24 c m$ ，点C是直线 $A B$ 上一点，且 $B C = k \cdot A C$ ，若点D是 $A C$ 的中点，求线段 $C D$ 的长．

查看试题解析
22. 如图1，A、O、B三点在同一直线上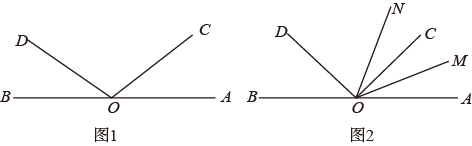， $∠ A O D$ 与 $∠ A O C$ 互补．

(1)、请判断 $∠ A O C$ 与 $∠ B O D$ 大小关系，并验证你的结论；

(2)、如图2， A、O、B三点在同一直线上， $∠ A O D$ 与 $∠ A O C$ 互补，若 $O M$ 平分 $∠ A O C$ ， $O N$ 平分 $∠ A O D$ ， $∠ B O D = 30 °$ ，请求出 $∠ M O N$ 的度数．

查看试题解析
23.

(1)、阅读材料：我们知道， $4 x + 2 x - x = (4 + 2 - 1) x = 5 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) + 2 (a + b) - (a + b) - (4 + 2 - 1) (a + b) = 5 (a + b)$ ． “整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．
尝试应用：
①把 $(a + b)$ 看成一个整体，合并 $- 3 (a + b)^{2} - 6 (a + b)^{2} + 8 (a + b)^{2}$ 的结果 ▲ ．
②拓广探索：已知 $a - 2 b = 5 ， 2 b - c = - 7 ， c - d = 12$ ，求 $4 (a - c) + 4 (2 b - d) - 4 (2 b - c)$ 的值．

(2)、某人用400元购买了8套电子产品，准备以一定价格出售，如果每套电子产品以56元的价格作为标准卖出，超出的记为正数，不足的记为负数，记录如下（单位：元）：
$- 3 ， + 7 ， - 8 ， + 9 ， - 2 ， 0 ， - 1 ， - 6$ ．
当他卖完这8套电子产品后是盈利还是亏损？

查看试题解析
24. 为了抗击新冠肺炎疫情，健民药店对消毒液和口罩开展优惠活动．消毒液每桶标价15元，口罩每包标价5元．现在药店有两种优惠方式：①按标价购买时，买一桶消毒液送一包口罩；②消毒液和口罩都按定价的80%付款．现在某单位要到该药店购买消毒液40桶，口罩x包 $(x > 40)$ ．

(1)、该单位按优惠方式①购买需要付款元（用含x的式子表示）；该单位按优惠方式②购买需要付款元（用含x的式子表示）．

(2)、试求当x取何值时，方式①和方式②的购买费用一样．

(3)、当 $x = 200$ 时，通过计算说明按哪个优惠方式购买最合适．

查看试题解析
25. 如图，已知数轴上A点表示的数为a，B点表示的数为b，O为原点．且满足 $a = | - 4 | + (- 2)^{4}$ ， b是单项式 $\frac{3 x^{4} y^{6} z^{2}}{5}$ 的次数的相反数．动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为 $m (m > 0)$ 秒．

(1)、求出数轴上点A表示的数和点B表示的数，用含的式子表示出数轴上点P表示的数；

(2)、当点P在点B的左侧运动时，M、N分别是线段 $P A$ 、 $P B$ 的中点，求 $P M - P N$ 的值；

(3)、动点Q从点B出发，以每秒2个单位长度的速度沿数轴向右匀速运动，若点P、Q同时出发，运动多少秒时P、Q两点重合，此时点P在数轴上的点对应的数值是多少？

查看试题解析