山东省滨州市博兴县2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-12-01 类型：期末考试

进入出卷网下载

一、单选题

1. 对于式子-（-5），下列表述：①表示-5的相反数；②表示-1与-5的积；③等于-5的绝对值；④计算结果等于5．其中表述正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 随着我国金融科技不断发展，网络消费、网上购物已成为人们生活不可或缺的一部分，今年“双十一”天猫成交额高达2684亿元.将数据“2684亿”用科学记数法表示（）

A、 $2.684 \times 10^{3}$ B、 $2.684 \times 10^{11}$ C、 $2.684 \times 10^{12}$ D、 $2.684 \times 10^{7}$

查看试题解析
3. 如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能符合题意解释这一现象的数学知识是（）

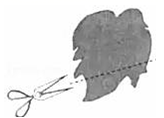A、垂线段最短 B、经过一点有无数条直线 C、两点之间，线段最短 D、经过两点，有且仅有一条直线

查看试题解析
4. 下列说法正确的是（）

A、 $- 2 a b^{2} c^{3}$ 与 $0.6 b^{2} c^{3} a$ 可以合并 B、 $\frac{2}{5} π x^{2}$ 的系数是 $\frac{2}{5}$ C、 $- 11 a^{2} b$ 的次数是2 D、 $3 a + 2 b + 1$ 是二次三项式

查看试题解析
5. 下列计算正确的是（）

A、 $2 c + 3 c = 5 c^{2}$ B、 $6 a^{2} b - 3 a b^{2} = 3 a b$ C、 $4 y^{2} - 2 y^{2} = 2 y^{2}$ D、 $6 b^{2} - 5 b^{2} = 1$

查看试题解析
6. 已知单项式 $m x^{2} y^{n - 1} 与 3 x^{2} y^{5}$ 是同类项，若 $m x^{2} y^{n - 1} + 3 x^{2} y^{5} = 0$ （其中 $x \neq 0 ， y \neq 0$ ），则 $m + n =$ （）

A、-3 B、3 C、5 D、10

查看试题解析
7. 下列运用等式的性质进行的变形中，正确的是（）

A、若 $a = b$ ，则 $a + c = b - c$ B、若 $\frac{a}{c} = \frac{b}{c}$ ，则 $a = b$ C、若 $a = b$ ，则 $\frac{a}{c} = \frac{b}{c}$ D、若 $a^{2} = 3 a$ ，则 $a = 3$

查看试题解析
8. 某车间28名工人生产螺栓和螺母，每人每天平均生产螺栓12个或螺母18个，一个螺栓需要两个螺母与之配套，如何安排生产螺栓才能让螺栓和螺母正好配套？设有x名工人生产螺栓，其余人生产螺母，依题意列方程应为（）

A、 $12 x = 18 (28 - x)$ B、 $2 \cdot 12 x = 18 (28 - x)$ C、 $12 \cdot 18 x = 18 (28 - x)$ D、 $12 x = 2 \cdot 18 (28 - x)$

查看试题解析
9. 已知线段MN，点P是直线MN上的一点，MN=10cm，NP=6cm，点E是线段MP的中点，则线段ME的长为（）

A、2cm B、4cm C、2cm或8cm D、4cm或8cm

查看试题解析
10. 某商店出售两件衣服，每件卖了100元，其中一件赚25%，而另一件赔20%．那么商店在这次交易中（）

A、赚了5元 B、赚了10元 C、亏了10元 D、亏了5元

查看试题解析
11. 已知a、b互为相反数，e的绝对值为 $3$ ， m与n互为倒数，则 $\frac{a + b}{3} + e^{2} - 9 m n$ 的值为（）

A、1 B、3 C、0 D、无法确定

查看试题解析
12. 已知50个整数 $a_{1} ， a_{2} ， a_{3} ， ⋯ ， a_{50}$ 满足下列条件： $a_{1} = - 1$ ， $a_{2} = - | a_{1} + 1 |$ ， $a_{3} = - | a_{2} + 1 |$ ， ……， $a_{50} = - | a_{49} + 1 |$ ，则 $a_{1} + a_{2} + a_{3} + ⋯ + a_{50} =$ （）

A、-25 B、 $0$ C、-50 D、50

查看试题解析

二、填空题

13. 若把 $30 ° 4 2^{'} 3 6^{″}$ 化成以度为单位，则结果为．

查看试题解析
14. 一个角的补角的2倍比它的余角的6倍少20°，则这个角的度数为．

查看试题解析
15. 若关于x的方程 $5 x + 4 a = 9$ 和方程 $\frac{1}{3} x - 4 = - 1$ 的解相同，则a的值为．

查看试题解析
16. 一个三位数，若个位数字为 $n + 2$ ，十位数字为n，百位数字为 $n + 3$ ，则这个三位数用含n的式子可表示为．

查看试题解析
17. 若多项式 $2 x^{2} + 3 x + 2$ 的值为5，则多项式 $6 x^{2} + 9 x - 1$ 的值为．

查看试题解析
18. 若有理数a、b、c在数轴上位置如图所示，则化简 $| c - a | - | a + b | + | b - c |$ 的结果为．

查看试题解析

三、解答题

19. 计算：

(1)、 $| - 3 | - (- 5) + 21 \div (- 3) - \frac{1}{2} \times (- 10)$ ；

(2)、 $(- 1)^{2022} + | (- 2)^{3} + (- 3)^{2} | - (- \frac{1}{4} + \frac{1}{6}) \times (- 24)$ ．

查看试题解析
20. 化简并求值：

(1)、 $(m^{2} + 5 m) - 3 (\frac{1}{3} m^{2} + 3 m)$ ，其中 $m = \frac{7}{8}$ ；

(2)、 $(2 a b^{2} - a) - \frac{1}{2} (b + 4 a b^{2}) - \frac{1}{3} (a^{2} b - \frac{3}{2} b - 3 a)$ ，其中a、b满足 $| a + 3 | + (b - 2)^{2} = 0$ ．

查看试题解析
21. 解方程：

(1)、 $x - \frac{x - 2}{2} = 1 + \frac{2 x - 1}{3}$ ；

(2)、 $\frac{x}{0.7} - \frac{0.17 - 0.2 x}{0.03} = 1$ ．

查看试题解析
22. 如图，点O在直线AB上， $∠ C O E$ 是直角，OF平分 $∠ A O E$ ， $∠ C O F = 30 °$ ，求 $∠ E O B$ 的大小．

查看试题解析
23. 某项工程，甲队单独干需10小时完成，乙队单独干则需20小时完成，丙队单独干则需30小时完成．开始时三队合作，一段时间后甲队有事离开，剩余工程由乙、丙两队合作完成，此项工程从开始到工作完成共用6小时，问甲队实际做了多少小时？

查看试题解析
24. 已知数轴上点A表示的数为8，点B是数轴上在点A左侧的一点，且A、B两点间的距离为12．动点P、Q分别从点A、B出发，沿数轴向左匀速运动，点P的速度为每秒4个单位长度，点Q的速度为每秒3个单位长度，设运动时间为t（t＞0）秒．

(1)、数轴上点B表示的数是，当点P运动到AB的中点时，它所表示的数是．

(2)、若点P、Q同时出发：
①当点P运动多少秒时，点P追上点Q？
②当点P运动多少秒时，点P与点Q间的距离为6个单位长度．

查看试题解析