浙江省温州市龙港市2022-2023学年九年级上学期期中数学试卷
试卷更新日期：2022-12-01 类型：期中考试
一、选择题（本题有10小题，每小题4分，共40分.）
-
1. 一般情况下，下列事件属于不确定事件的是（ ）A、三角形的内角和等于180° B、任意抛掷一枚一元硬币，结果正面朝上 C、抛出去的篮球会下落 D、从一个只装有白球的袋子中摸出红球2. 在同一平面内，已知⊙O的半径为3cm，OP＝4cm，则点P与⊙O的位置关系是（ ）A、点P在⊙O圆外 B、点P在⊙O上 C、点P在⊙O内 D、无法确定3. 学校招募运动会广播员，从三名男生和一名女生中随机选取一人，则选中女生的概率是（ ）A、 B、 C、 D、4. 将抛物线y＝3x2向左平移2个单位后所得抛物线的表达式是（ ）A、y＝3（x+2）2 B、y＝（3x−2）2 C、y＝3x2+2 D、y＝3x2−25. 如图，⊙O的弦AB＝8，M是AB的中点，且OM＝3，则⊙O的半径等于（ ）
A、 B、4 C、5 D、66. 已知在圆的内接四边形ABCD中，∠A：∠B：∠C＝2：3：7，则∠D等于（ ）A、40° B、60° C、100° D、120°7. 二次函数y＝ax2+bx+c图象的一部分如图所示，它与x轴的一交点为B（6，0），对称轴为直线x＝2，则由图象可知，方程ax2+bx+c＝0的解是（ ）
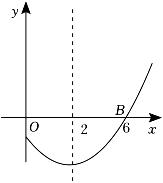A、x1＝0，x2＝6 B、x1＝-2，x2＝6 C、x1＝-1，x2＝6 D、x1＝-2，x2＝28. 将进货价格为35元的商品按单价40元售出时，能卖出200个.已知该商品单价每上涨1元，其销售量就减少5个.设这种商品的售价上涨x元时，获得的利润为y元，则下列关系式正确的是（ ）A、y＝（x-35）（200-5x） B、y＝（x+40）（200−10x） C、y＝（x+5）（200-5x） D、y＝（x+5）（200−10x）9. 如图所示，在△ABC中，∠ACB＝90°，∠ABC＝28°.将△ABC绕点B逆时针方向旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠CAA′等于（ ）
A、138° B、134° C、124° D、118°10. 已知点（m-3，y1），（m，y2）都在二次函数y＝（x-2）2+n的图象上.若y1＞y2 ， 则m的取值范围为（ ）A、m＞2 B、m＜2 C、m＞ D、m＜二、填空题（本大题共6小题，每小题5分，共30分）
-
11. 已知二次函数y＝ax2的图象开口向上，请写出一个符合条件的a的值：.12. 在一个不透明的袋中装有除颜色外完全相同的a个小球，其中红球的个数为2，随机摸出一个球记下颜色后再放回袋中，通过大量重复实验发现，摸到红球的频率稳定于0.1附近，那么可以推算出a的值大约是 ．13. 如图，四边形ABCD是⊙O的内接正方形，E是的中点，AE交BC于点F，则∠1＝度.
14. 在直径为60cm的圆柱形油罐内装进一些油后，其横截面如图所示，若油面宽AB＝48cm，则油的最大深度为cm.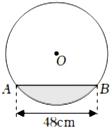
15. 如图，利用135°的墙角修建一个四边形ABCD的花坛，使得AD∥BC，∠C＝90°，如果新建围墙折线B-C-D总长15米，那么当CD＝米时，花坛的面积会达到最大.
16. 如图，在以AB为直径的半圆O上，AB＝2 ， 点C是半圆弧上的任意点，点F是的中点，连结BF交AC于点E，AD平分∠CAB交BF于点D，则∠ADB＝度；当DB＝DF时，BC的长为.
三、解答题（本题有8小题，共80分）
-
17. 小乐从标有1到20数字的20张相同的卡片中任取一张.(1)、求抽到的卡片的数字是5的倍数的概率.(2)、求抽到的卡片的数字既是2的倍数，又是5的倍数的概率.18. 如图，在单位长度为1的正方形网格中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格图中进行下列操作（以下结果保留根号）：
(1)、利用网格作出该圆弧所在圆的圆心D点的位置，并写出D点的坐标为 ▲ ；(2)、连接AD、CD，则⊙D的半径为 ， ∠ADC的度数为.19. 已知：如图，在⊙O中，∠ABD＝∠CDB.求证：AB＝CD.
20. 某社区举行新冠疫情防控核酸检测，卫生防疫部门在该社区设置了三个检测点A，B，C，甲、乙两人可以任意选择一个检测点检测.(1)、求甲在A检测点或B检测点检测的概率.(2)、求甲、乙两人选择同一个检测点的概率（用树状图或列表的方法求解）.21. 如图，已知抛物线y＝x2+5x+4交x轴于点A（点A在该抛物线对称轴的左侧），交y轴于点B，AB交抛物线对称轴于点P.
(1)、求证：OA＝OB.(2)、求点P的坐标.22. 如图，AB是⊙O的直径，点C在⊙O上，延长BC至点D，使得DC＝CB，延长DA交⊙O于另一个点E，连结AC，CE.
(1)、求证：∠D＝∠E.(2)、若AD＝5，AE＝3，求CE的长.23. 根据以下素材，探索完成任务.如何设计高架桥的限高及车道宽方案？
素材1
图1高架桥是一段圆弧拱形结构，图2是它的示意图.经测量，拱形跨度24m，拱顶离地面6m.
素材2
如图3，某道路规划部门计划将左侧公路分为非机动车道、机动车道一、机动车道二及绿化带四部分，原计划设计非机动车道宽3m，每条机动车道宽均3.5m.为了保证车辆的行驶安全，高架下方需要设置限高标志以警示车辆驾驶员.（限高即图中FC的高度）
素材3
如图4，由于城市道路绿化需求，道路规划部门确定新方案为在非机动车道和机动车道一之间增加一条宽为1m的绿化带，中间绿化带宽度不变，每条机动车道道宽均不小于3.25m且相等，非机动车道最高高度不小于2.5m.
问题解决
任务1
确定桥拱所在圆弧的半径.
在图2中补好图形，标注字母、数据等信息，求出桥拱所在圆弧的半径长.
任务2
探究原计划该高架桥下方机动车道一的限高要求.
在图3中画出图形，标注字母、数据等信息，计算确定机动车道一的限高高度.
任务3
拟定新方案下非机动车道和机动车车道宽度.
给出一对符合新方案要求的非机动车道和机动车道的道宽值.
（参考数值：＝9.63，＝11.61）
24. 如图，抛物线y＝−x2+bx+c经过点A（-1，0），点B（3，0），与y轴交于点C，点D在射线CO上运动.
(1)、求该抛物线的表达式和对称轴.(2)、过点D作x轴的平行线交抛物线于点E，F（点E在点F的左侧），若EF＝2OC，求点E的坐标.(3)、记抛物线的顶点关于直线EF的对称点为点P，当点P到x轴的距离等于1时，求出所有符合条件的线段EF的长.