浙江省温州市龙港市2022-2023学年八年级上学期期中数学试卷
试卷更新日期：2022-12-01 类型：期中考试
一、选择题（本题有10小题，每小题3分，共30分.）
-
1. 下列图形分别是无公害食品、绿色食品、有机食品和安全食品的图标，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 在△ABC中，∠A＝50°，∠B＝70°，则∠C的度数是（ ）A、40° B、60° C、80° D、100°3. 已知三角形的两条边长分别等于4cm和9cm，则第三边的长可能是（ ）A、4cm B、5cm C、9cm D、13cm4. 可以用来说明命题“若a＞b，则|a|＞|b|”是假命题的反例是（ ）A、a＝0，b＝-1 B、a＝1，b＝0 C、a＝2，b＝1 D、a＝2，b＝-15. 如图，已知∠BDA＝∠CDA，要使△ABD与△ACD全等，则添加的条件可以是（ ）
A、∠BAD＝∠CAD B、AB＝AC C、BD＝AC D、∠B＝∠DAC6. 如图，上午8时，渔船从A处出发，以20海里/时的速度向正西方向航行，9时30分到达B处.从A处测得灯塔C在南偏西30°方向，距A处30海里处.则B处到灯塔C的距离是（ ）
A、20海里 B、25海里 C、30海里 D、35海里7. 分别以下列四组数作为三角形的边长，其中能构成直角三角形的是（ ）A、 ， ， B、 ， ， C、2，3，4 D、9，12，158. 已知等腰三角形的一个内角是30°，那么这个等腰三角形顶角的度数是（ ）A、75° B、120° C、30° D、30°或120°9. 如图，将等边△ABC折叠，使得点C落在AB边上的点D处，EF是折痕，若∠ADE＝90°，AD＝1，则AC的长是（ ）
A、2 B、4 C、2 D、2+10. 三国时期的赵爽利用图1证明了勾股定理，后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中，E，B，F在同一条直线上，四边形ABCD，EFGA，HGDJ都是正方形，若正方形ABCD的面积等于100，△IJD面积等于 ， 且已知AH＝2，则△KCD的面积等于（ ）
A、 B、39 C、 D、52二、填空题（本题有8小题，每小题3分，共24分）
-
11. 写出命题“两直线平行，内错角相等”的逆命题： ．12. 如图，AD是等腰△ABC的顶角平分线，BD＝5，则CD＝.
13. 直角三角形两直角边长为5和12，则此直角三角形斜边上的中线的长是 ．14. 如图所示，在△ABC中，AD为△ABC的中线， E为AD的中点．若△ABC的面积为4，则△AEC的面积为 ．
15. 如图，点P是∠AOC的角平分线上一点，PD⊥OA，垂足为点D，且PD＝3，点M是射线OC上一动点，则PM的最小值为.
16. 如图，已知AD，CE是△ABC的两条高线，AD＝CE，∠CAD＝25°，则∠OCD＝度.
17. 如图，在△ABC中，∠ACB＝90°，AC＜BC.分别以点A，B为圆心，大于 AB的长为半径画弧，两弧交于D，E两点，直线DE交BC于点F，连接AF.以点A为圆心，AF为半径画弧，交BC延长线于点H，连接AH.若BC＝3，则△AFH的周长为 .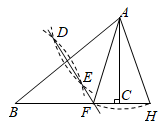
18. 商场卫生间旋转门锁的局部图如图1所示，图2是其工作简化图.锁芯O固定在距离门边（即EF）3.5cm处（即OD＝3.5cm），在自然状态下，把手竖直向下（把手底端到达A处）.旋转一定角度，使得把手底端B恰好卡在门边，此时底端A，B的竖直高度差为0.5cm，则OB的长度是cm.当把手旋转到OC⊥OB时，点C与点B的高度差BH是cm.
三、解答题（本题有6小题，共46分.）
-
19. 已知：如图，AC＝BD，AD＝BC.求证：∠C＝∠D.
20. 如图，AE，AD分别是△ABC的高线和角平分线，且∠B＝40°，∠C＝60°，求∠DAE的度数.
21. 方格纸中小正方形的顶点叫格点，点A和点B是格点，位置如图.
(1)、在图1中确定格点C，使得△ABC是直角三角形，画出一个这样的△ABC，并直接写出线段AB的长.(2)、在图2中确定格点D，使得△ABD是等腰三角形，画出一个这样的△ABD.22. 如图，△ABC是等边三角形，点D是边AB上一点，以CD为边向上作等边△CDE，连结AE.
(1)、求证：△BCD≌△ACE.(2)、若AE＝1，AB＝3，求AD的长.23. 根据以下素材，探索完成任务.三角形背景下角的关系探索
素材1
如图，已知等腰△ABC中，BA＝BC，在腰BC的延长线上取点E，连结AE，作AE的中垂线交射线BC于点D，连结AD.
素材2
研究一个几何问题时，一般先根据几何语言画出几何图形.可能需要分类讨论.
素材3
当我们要论证一个一般性结论时，常常将问题先分成几种特例，在研究特例的过程中寻求规律，总结方法，猜测结论，再将规律、方法和结论迁移到一般情形中，这种数学推理方法叫做归纳法.
问题解决
任务1
补全图形
请根据素材1，把图形补全.你画的点D在点C的 ▲ 侧.
任务2
特例猜想
有下列条件：①AB＝AC；②∠B＝40°；③∠CEA＝20°；④∠CEA＝50°；请从中选择你认为合适的一个或两个条件作为已知条件，求出∠BAD和∠CAE的大小，并猜测∠BAD与∠CAE的数量关系.
任务3
一般结论
请根据你在任务1中所画的一般情况下的图形，写出∠BAD与∠CAE的数量关系，并说明理由.
任务4
拓展延伸
除了你在任务1中所画的情形外，点D相对于点C的位置还有不同的情形吗？若有，请画出图形，并直接写出∠BAD与∠CAE的数量关系.
24. 如图，在△ABC中，AC＝BC＝ ， ∠ACB＝120°，将一块足够大的直角三角尺PEF（∠E＝90°，∠EPF＝30°）按如图放置，顶点P在线段AB上滑动（不与点A，B重合），三角尺的直角边PE始终经过点C，斜边PF交AC于点D.
(1)、当PD∥BC时，判断△BCP的形状，并说明理由；(2)、当△PCD是等腰三角形时，求出所有满足要求的BP的长；(3)、记点C关于PD的对称点为C′，当C′D⊥AC时，AP的长是.