浙江省宁波市鄞州区七校联考2022-2023学年七年级上学期期中数学试卷

试卷更新日期：2022-12-01 类型：期中考试

进入出卷网下载

一、单选题（每小题3分，共30分）

1. -2022的相反数是（）

A、- $\frac{1}{2022}$ B、 $\frac{1}{2022}$ C、-2022 D、2022

查看试题解析
2. 我国的陆地面积为9600000平方千米，9600000用科学记数法可表示为（）

A、 $96 \times 1 0^{5}$ B、 $9.6 \times 1 0^{6}$ C、 $0.96 \times 1 0^{7}$ D、 $960 \times 1 0^{4}$

查看试题解析
3. 如果x是有理数，那么下列各式中一定比0大的是（）

A、2021-x B、2021+x C、|x|+2021 D、|x|

查看试题解析
4. 在实数： $π ， \sqrt{2} ， \frac{22}{7} ， \sqrt[3]{27} ， 0.1010010001 \dots$ (每2个1之间依次多一个0 ) 中，无理数的个数是（）

A、1 个 B、2 个 C、3 个 D、4 个

查看试题解析
5. 实数 $\sqrt{5}$ 在哪两个相邻的整数之间（）

A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间

查看试题解析
6. 如图，面积为5的正方形ABCD的顶点A在数轴上，且表示的数为1，若点E在数轴上，（点E在点A的右侧）且AB＝AE，则E点所表示的数为（）

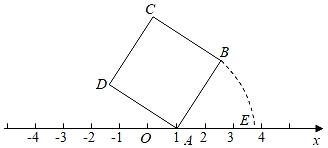A、 $\sqrt{5}$ B、1+ $\sqrt{5}$ C、 $\frac{2 + \sqrt{5}}{2}$ D、 $\sqrt{5}$ +2

查看试题解析
7. 已知|x|＝6，y²＝4，且xy＜0.则x+y的值为（）

A、4 B、-4 C、4或-4 D、2或-2

查看试题解析
8. 已知：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，…，那么2²⁰²¹的个位数字是（）

A、2 B、4 C、6 D、8

查看试题解析
9. 若abc≠0，则 $\frac{| a |}{a}$ ＋ $\frac{| b |}{b}$ + $\frac{c}{| c |}$ 的值为（）

A、±3或±1 B、±3或0或±1 C、±3或0 D、0或±1

查看试题解析
10. 如果一个正数x的平方根是2a-3和5-a，那么x的值是（）

A、-2 B、7 C、-7 D、49

查看试题解析

二、填空题（每题4分，共24分）

11. -1 $\frac{2}{3}$ 的倒数等于.

查看试题解析
12. 已知a+3b-4＝0，则9b+3a-11的值是 .

查看试题解析
13. 已知a是 $\sqrt{10}$ 的整数部分，b是它的小数部分，则2a+b- $\sqrt{10}$ ＝.

查看试题解析
14. 若“！”是一种数学运算符号，并且：1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1＝24，…，则 $\frac{100 ！}{98 ！}$ ＝.

查看试题解析
15. 数轴上表示1， $\sqrt{3}$ 的对应点分别为点A，点B.若点B关于点A的对称点为点C，则点C所表示的数为.

查看试题解析
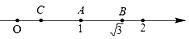16. 如图，将直径为1个单位长度的圆沿着数轴向右滚动一周，圆上一点由表示﹣2的点A到达点A'，则点A'对应的数是．

查看试题解析

三、解答题（共8题，共66分）

17. 计算：

(1)、-2+（-7）-3+8；

(2)、-1²⁰²¹+（ $\frac{1}{2} - \frac{1}{3}$ ）×|-6|÷2²；

(3)、 $(\frac{1}{4} - \frac{2}{3} - \frac{5}{6}) \times (- 12)$ ；

(4)、 $- 2^{3} + \sqrt[3]{- 27} - (- 2)^{2} \div \sqrt{\frac{16}{81}}$ .

查看试题解析
18. 在如图所示的方格中，按要求画出相应面积的正方形，要求正方形的每个顶点在方格图的格点.

查看试题解析
19. 已知实数a，b，c满足： $\sqrt{a + 2} + | b - 3 | + (c - 1)^{2} = 0$ ，求（a+b+c）²的值.

查看试题解析
20. 已知a、b互为相反数（a，b不为0），c、d互为倒数，|m|＝2，且m＞0，求2a+2b+ $\frac{a}{b}$ -（cd）²⁰²²-3m的值.

查看试题解析
21. 出租车司机小张某天上午的营运全是在东西方向的大道上运行的，若规定向东为正，向西为负，他这天上午的行车里程如下：10，-3，4，-1，8，-7，-3，14，3，-4，（单位：km）.

(1)、将最后一名乘客送到目的地时，小张离最开始的出发点有多远？在出发点的哪个方向？

(2)、若汽车的耗油量是每千米耗油a（1），这天上午小张共耗油多少升？

查看试题解析
22. 初中阶段，目前我们已经学习了多种计算技巧，例如裂项相消法，错位相减法等等，请计算下列各式：

(1)、 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + + \frac{1}{+ 2019 \times 2021}$ ＝；

(2)、 $\frac{1}{1 \times 4} + \frac{1}{4 \times 7} + \frac{1}{7 \times 10} + + \frac{1}{\to 2020 \times 2023}$ ＝；

(3)、 $| 1 - \sqrt{2} | + | \sqrt{2} - \sqrt{3} | + | \sqrt{3} - \sqrt{4} | + + | \sqrt{2021} - \sqrt{2022} |$ ＝.

查看试题解析
23. “数形结合”是重要的数学思想.如：|3-（-2）|表示3与-2差的绝对值，实际上也可以理解为3与-2在数轴上所对应的两个点之间的距离.进一步地，数轴上两个点A，B所对应的数分别用a，b表示，那么A，B两点之间的距离表示为AB＝|a-b|.利用此结论，回答以下问题：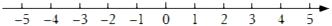

(1)、数轴上-2和5这两点之间的距离为.

(2)、若x表示一个实数，|x+2|+|x-4|的最小值为.

(3)、直接写出所有符合条件的x，使得|x-2|+|x+5|＝9，则x的值为.

查看试题解析
24. 为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的价目表如表（注：水费按一个月结算一次）：请根据价目表的内容解答下列问题：
每月用水量（m³）
单价（元/m³）
不超出26m³的部分
3
超出26m³不超出34m³的部分
4
超出34m³的部分
7

(1)、填空：若该户居民1月份用水20立方米，则应收水费元；若该户2月份用水30立方米，则应收水费元；

(2)、若该户居民3月份用水x立方米（其中26＜x≤34），则应收水费多少元？（结果用含x的代数式表示）

(3)、若该户居民3月份用水a立方米（其中a＞34），则应收水费多少元？（结果用含a的代数式表示）

查看试题解析

每月用水量（m³）	单价（元/m³）
不超出26m³的部分	3
超出26m³不超出34m³的部分	4
超出34m³的部分	7