浙江省宁波市鄞州区七校联考2022-2023学年九年级上学期期中数学试卷
试卷更新日期:2022-12-01 类型:期中考试
一、选择题(本大题共10小题,共40.0分。)
-
1. 已知的半径为5,若 , 则点与的位置关系是
 ( ) A、点在内 B、点在上 C、点在外 D、无法判断2. 下列事件中,属于必然事件的是( )A、掷一枚硬币,正面朝下 B、三角形两边之和大于第三边 C、一个三角形三个内角的和小于180° D、在一个没有红球的盒子里,摸到红球3. 由二次函数 , 可知( )A、其图象的对称轴为直线 B、其最大值为1 C、当时,随的增大而增大 D、其图象与轴的交点为4. 已知二次函数 , 用配方法化为的形式,结果是( )A、 B、 C、 D、5. 如图,已知是的直径,弦于点 , 是的中点,连结 , , , 则下列结论不一定成立的是( )
( ) A、点在内 B、点在上 C、点在外 D、无法判断2. 下列事件中,属于必然事件的是( )A、掷一枚硬币,正面朝下 B、三角形两边之和大于第三边 C、一个三角形三个内角的和小于180° D、在一个没有红球的盒子里,摸到红球3. 由二次函数 , 可知( )A、其图象的对称轴为直线 B、其最大值为1 C、当时,随的增大而增大 D、其图象与轴的交点为4. 已知二次函数 , 用配方法化为的形式,结果是( )A、 B、 C、 D、5. 如图,已知是的直径,弦于点 , 是的中点,连结 , , , 则下列结论不一定成立的是( ) A、 B、 C、 D、6. 下列说法正确的是( )A、半圆是弧,弧也是半圆 B、三点确定一个圆 C、平分弦的直径垂直于弦 D、直径是同一圆中最长的弦7. 如图,⊙O的半径为10,若OP=8,则经过点P的弦长可能是( )
A、 B、 C、 D、6. 下列说法正确的是( )A、半圆是弧,弧也是半圆 B、三点确定一个圆 C、平分弦的直径垂直于弦 D、直径是同一圆中最长的弦7. 如图,⊙O的半径为10,若OP=8,则经过点P的弦长可能是( )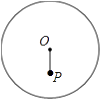 A、10 B、6 C、19 D、228. 、、是抛物线上三点, , , 的大小关系为( )A、1 B、 C、 D、9. 如图,抛物线的对称轴为直线 , 与轴的一个交点坐标为 , 其部分图象如图所示,下列结论:
A、10 B、6 C、19 D、228. 、、是抛物线上三点, , , 的大小关系为( )A、1 B、 C、 D、9. 如图,抛物线的对称轴为直线 , 与轴的一个交点坐标为 , 其部分图象如图所示,下列结论:
;方程的两个根是 , ;;
当时,的取值范围是;当时,随增大而增大.
其中结论正确的个数是( )
A、4个 B、3个 C、2个 D、1个10. 如图,是的直径,点 , 点是半圆上两点,连结 , 相交于点 , 连结 , 已知于点 , 下列结论:
;若点为的中点,则.若 , 则;;其中正确的是( )
A、 B、 C、 D、二、填空题(本大题共6小题,共30.0分)
-
11. 从这9个自然数中任取一个,是2的倍数的概率是.12.
如图所示,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=54°,则∠BCD= .
 13. 五水共治办公室在一次巡查时测量一排水管的排水情况,如图,水平放置的圆柱形排水管的截面为 , 半径是 , 有水部分弓形的高为 , 则.
13. 五水共治办公室在一次巡查时测量一排水管的排水情况,如图,水平放置的圆柱形排水管的截面为 , 半径是 , 有水部分弓形的高为 , 则. 14. 把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的表达式为.15. 某一型号飞机着陆后滑行的距离单位:与滑行时间单位:之间的函数关系式是 , 该型号飞机着陆后滑行才能停下来.16. 如图,在平面直角坐标系xOy中,半径为4的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为.
14. 把抛物线向左平移1个单位,然后向上平移3个单位,则平移后抛物线的表达式为.15. 某一型号飞机着陆后滑行的距离单位:与滑行时间单位:之间的函数关系式是 , 该型号飞机着陆后滑行才能停下来.16. 如图,在平面直角坐标系xOy中,半径为4的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点,点C为弦AB的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为.
三、解答题(本大题共8小题,共80.0分。)
-
17. 一个不透明的袋中装有分别标着汉字“温”“外”“数”“学”的4个小球,除汉字不同之外,小球材质、大小、形状全部相同,每次摸球前先搅拌均匀再摸球.(1)、求从袋中摸出一个球,则球上的汉字刚好是“温”的概率是;(2)、从袋中任取一球,不放回,再从袋中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字恰能组成“数学”的概率.18. 如图,在的正方形网格中每个小正方形的边长都为1个单位 , 的三个顶点都在格点上.建立如图所示的直角坐标系,

⑴请在图中标出的外接圆的圆心的位置;并填写:圆心的坐标: ▲ , ▲ )
⑵将绕点逆时针旋转得到 , 请画出 , 并保留作图痕迹.
19. 已知某二次函数图象的顶点坐标为 , 且经过点.(1)、求这个二次函数的表达式;(2)、求图象与轴交点、两点的坐标在点的左边及的面积.20. 已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.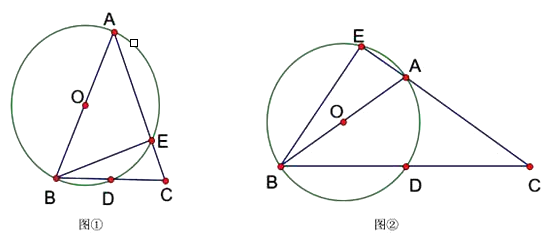 (1)、当∠BAC为锐角时,如图①,求证:∠CBE=(2)、当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.21. 台风是一种自然灾害,它以台风中心为圆心在周围数十千米的范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市的正南方向的处有一台风中心,该台风中心现在正以的速度沿北偏东方向移动,若在距离台风中心范围内都要受到影响.结果精确到
(1)、当∠BAC为锐角时,如图①,求证:∠CBE=(2)、当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.21. 台风是一种自然灾害,它以台风中心为圆心在周围数十千米的范围内形成气旋风暴,有极强的破坏力,据气象观测,距沿海某城市的正南方向的处有一台风中心,该台风中心现在正以的速度沿北偏东方向移动,若在距离台风中心范围内都要受到影响.结果精确到 (1)、该城市是否会受到这次台风的影响?说明理由.(2)、若会受到台风影响,那么台风影响该城市的持续时间有多长?22. 某超市经销一种销售成本为每件60元的商品,据市场调查发现,如果按每件70元销售,一周能售出500件,若销售单价每涨1元,每周销售就减少10件,设销售价为每件元 , 一周的销售量为件.(1)、当销售价为每件80元时,一周能销售多少件;答:件;(2)、写出与的函数关系式;(3)、设一周的销售利润为 , 当销售价定为多少元时,周销售利润达到了最大值,最大值是多少元?(4)、在超市对该种商品投入不超过18000元的情况下,使得一周销售利润达到8000元,销售单价应定为多少元?23. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)、该城市是否会受到这次台风的影响?说明理由.(2)、若会受到台风影响,那么台风影响该城市的持续时间有多长?22. 某超市经销一种销售成本为每件60元的商品,据市场调查发现,如果按每件70元销售,一周能售出500件,若销售单价每涨1元,每周销售就减少10件,设销售价为每件元 , 一周的销售量为件.(1)、当销售价为每件80元时,一周能销售多少件;答:件;(2)、写出与的函数关系式;(3)、设一周的销售利润为 , 当销售价定为多少元时,周销售利润达到了最大值,最大值是多少元?(4)、在超市对该种商品投入不超过18000元的情况下,使得一周销售利润达到8000元,销售单价应定为多少元?23. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答: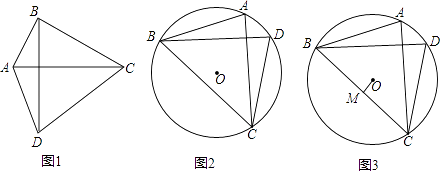 (1)、矩形 “奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.24. 一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米.
(1)、矩形 “奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.24. 一座桥如图,桥下水面宽度AB是20米,高CD是4米.要使高为3米的船通过,则其宽度须不超过多少米. (1)、如图1,若把桥看做是抛物线的一部分,建立如图坐标系.
(1)、如图1,若把桥看做是抛物线的一部分,建立如图坐标系.①求抛物线的解析式; ②要使高为3米的船通过,则其宽度须不超过多少米?
(2)、如图2,若把桥看做是圆的一部分.①求圆的半径;②要使高为3米的船通过,则其宽度须不超过多少米?