浙江省杭州市萧山区城区六校2022-2023学年九年级上学期期中数学试卷

试卷更新日期：2022-12-01 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。）

1. 二次函数 $y = - (x - 1)^{2} + 2$ 的顶点坐标为（）

A、 $(1 ， 2)$ B、 $(- 1 ， 2)$ C、 $(1 ， - 2)$ D、 $(- 1 ， - 2)$

查看试题解析
2. 从n个苹果和3个雪梨中，任选1个，若选中苹果的概率是 $\frac{1}{2}$ ，则n的值是（）

A、6 B、3 C、2 D、1

查看试题解析
3. 将抛物线 $y = 3 x^{2}$ 向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（）

A、 $y = 3 {(x + 2)}^{2} + 3$ B、 $y = 3 {(x - 2)}^{2} + 3$ C、 $y = 3 {(x + 2)}^{2} - 3$ D、 $y = 3 {(x - 2)}^{2} - 3$

查看试题解析
4. 对于 $y = - x^{2}$ 下列说法不正确的是（）

A、开口向下 B、对称轴为直线 $x = 0$ C、顶点为 $(0 ， 0)$ D、 $y$ 随 $x$ 增大而减小

查看试题解析
5. 已知圆 $O$ 的面积为 $25 π$ ，设点 $P$ 到圆心 $O$ 的距离为 $d$ ，若点 $P$ 不在圆 $O$ 内，则 $d$ 的长（）

A、 $d = 5$ B、 $0 \leq d < 5$ C、 $d > 5$ D、 $d \geq 5$

查看试题解析
6.
如图，AB是⊙O的直径，AB⊥CD于E，AB=10，CD=8，则BE为（）

A、2 B、3 C、4 D、3.5

查看试题解析
7. 如图，点 $A$ 、 $B$ 、 $C$ 、 $D$ 、 $E$ 都是 $⊙ O$ 上的点， $\overset{⌢}{A C} = \overset{⌢}{A E}$ ， $∠ D = 130 °$ ，则 $∠ B$ 的度数为（）

A、 $130 °$ B、 $128 °$ C、 $115 °$ D、 $116 °$

查看试题解析
8. 下列语句： $①$ 长度相等的弧是等弧； $②$ 过平面内三点可以作一个圆； $③$ 平分弦的直径垂直于弦； $④ 90 °$ 的圆周角所对的弦是直径； $⑤$ 等弦对等弧.其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图， $A B$ 为 $⊙ O$ 的直径，点 $C$ 为圆上一点，将劣弧 $A C$ 沿弦 $A C$ 翻折交 $A B$ 于点 $D$ ，连结 $C D$ ，点 $D$ 与圆心 $O$ 不重合， $∠ B A C = 26 °$ ，则 $∠ D C A$ 的度数为（）

A、 $38 °$ B、 $40 °$ C、 $42 °$ D、 $44 °$

查看试题解析
10. 已知二次函数 $y = - x^{2} - 2 (b - 2) x - b^{2} + 1$ 的图象不经过第二象限，则实数 $b$ 的取值范围是（）

A、 $b \geq \frac{5}{4}$ B、 $b \geq 1$ 或 $b \leq - 1$ C、 $b \geq 2$ D、 $1 \leq b \leq 2$

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 抽屉里放有3张黑桃和1张红桃共四张扑克牌.从中任意摸出1张，记下花色后不放回，再摸出1张.摸出的两张扑克牌颜色相同的概率是.

查看试题解析
12. 将二次函数 $y = x^{2} - 4 x + 5$ 化成 $y = a (x - h)^{2} + k$ 的形式为为.

查看试题解析
13. 直径为10的 $⊙ O$ 中有一条长度为 $5$ 的弦，则此弦所对的圆周角的度数为.

查看试题解析
14. 如图，平面直角坐标系中，二次函数 $y = x^{2} - 4 x + 3$ 的图象与 $x$ 轴交于点 $A$ ， $B$ ，以第一象限内点 $C$ 为圆心半径为2的圆经过 $A$ 、 $B$ 两点，则点 $C$ 的坐标为.

查看试题解析
15. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与 $x$ 轴交于点 $A (1 ， 0)$ 和 $B$ ，与 $y$ 轴的正半轴交于点 $C$ ，下列结论： $① a b c > 0$ ； $② 4 a - 2 b + c > 0$ ； $③ 2 a - b > 0$ ； $④ a - b \geq m (a m + b)$ ，其中所有正确结论的序号是.

查看试题解析
16. 如图，在半圆 $O$ 中半径为 $\sqrt{14}$ ， $\overset{⌢}{M C} = \frac{1}{3} \overset{⌢}{A C}$ ， $\overset{⌢}{N C} = \frac{1}{3} \overset{⌢}{B C}$ ， $B M$ 与 $A N$ 交于点 $D$ ，

(1)、 $∠ A D M =$ ；

(2)、当点 $D$ 恰好为 $B M$ 的中点时， $A M =$ .

查看试题解析

三、解答题（本大题共7小题，共66.0分。）

17. 已知一个二次函数 $y = x^{2} + b x + c$ 的图象经过点 $(2 ， 2)$ 和 $(1 ， 5)$ .

(1)、求这个二次函数的解析式；

(2)、求这个二次函数图象的顶点坐标和对称轴.

查看试题解析
18. 某商店准备销售 $A$ 、 $B$ 、 $C$ 、 $D$ 四种口味的牛奶，现经过一周试销后统计： $A$ 口味35箱， $B$ 口味40箱， $C$ 口味15箱， $D$ 口味10箱.

(1)、试估计某顾客购买 $B$ 口味的牛奶概率；

(2)、若商店为准备“双十一”促销活动，若根据试销的情况进货2000箱，这批牛奶中 $C$ 口味的牛奶大概多少箱？

查看试题解析
19. 如图， $⊙ O$ 的弦 $A B . C D$ 的相交于点 $P$ ，且 $A B = C D$ .
求证： $P A = P C$ .

查看试题解析
20. 在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=xm．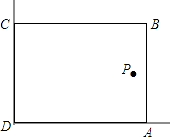

(1)、若花园的面积为192m² ，求x的值；

(2)、若在P处有一棵树与墙CD，AD的距离分别是15m和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值．

查看试题解析
21. 已知 $A B$ 是 $⊙ O$ 的直径，点 $C$ 在 $⊙ O$ 上， $D$ 为 $\overset{⌢}{B C}$ 的中点.
（Ⅰ）如图 $①$ ，连接 $A C$ ， $A D$ ， $O D .$ 求证： $O D / / A C$ ；
（Ⅱ）如图2，过点 $D$ 作 $D E ⊥ A B$ 交 $⊙ O$ 于点 $E$ ，直径 $E F$ 交 $A C$ 于点 $G$ ，若 $G$ 为 $A C$ 中点， $⊙ O$ 的半径为2，求 $A C$ 的长.

查看试题解析
22. 已知二次函数 $y = x^{2} - 2 m x + 2 m^{2} - 2$ .

(1)、若 $m = 2$ ，则该抛物线的对称轴为；若 $A (m - 2 ， y_{1})$ ， $B (m + 1 ， y_{2})$ 两点在该二次函数图象上，则 $y_{1}$ 与 $y_{2}$ 的大小关系为；

(2)、若该函数图象的顶点到 $x$ 轴的距离等于2，试求 $m$ 的值；

(3)、若抛物线在 $1 \leq x \leq 3$ 时，对应的函数有最大值3，求 $m$ 的值.

查看试题解析
23. 如图， $A B$ 为 $⊙ O$ 的直径，点 $C$ 、 $D$ 都在 $⊙ O$ 上，且 $C D$ 平分 $∠ A C B$ ，交 $A B$ 于点 $E$ .

(1)、求证： $∠ A B D = ∠ B C D$ ；

(2)、若 $D E = 13$ ， $A E = 17$ ，求 $⊙ O$ 的半径；

(3)、 $D F ⊥ A C$ 于点 $F$ ，试探究线段 $A F$ 、 $D F$ 、 $B C$ 之间的数量关系，并说明理由.

查看试题解析