四川省攀枝花市2022年中考数学试卷
试卷更新日期:2022-12-01 类型:中考真卷
一、单选题
-
1. 实数2的平方根为( )A、2 B、 C、 D、
-
2. 下列各式不是单项式的为( )A、3 B、a C、 D、
-
3. 下列计算正确的是( )A、 B、 C、 D、
-
4. 如图是由5个相同的正方体搭成的几何体,这个几何体的俯视图是( )
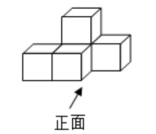 A、
A、 B、
B、 C、
C、 D、
D、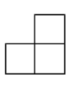
-
5. 实数a、b在数轴.上的对应点位置如图所示,下列结论中正确的是( )
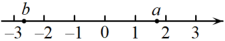 A、 B、 C、 D、
A、 B、 C、 D、 -
6. 若点在第一象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
7. 若关于x的方程有实数根,则实数m的取值的范围是( )A、 B、 C、 D、
-
8. 为深入落实“立德树人”的根本任务,坚持德、智、体、美、劳全面发展,某学校积极推进学生综合素质评价改革,某同学在本学期德智体美劳的评价得分如图所示,则该同学五项评价得分的众数,中位数,平均数分别为( )
 A、8,8,8 B、7,7,7.8 C、8,8,8.6 D、8,8,8.4
A、8,8,8 B、7,7,7.8 C、8,8,8.6 D、8,8,8.4 -
9. 如图,正比例函数与反比例函数的图象交于、B两点,当时,x的取值范围是( )
 A、或 B、或 C、或 D、或
A、或 B、或 C、或 D、或 -
10. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )
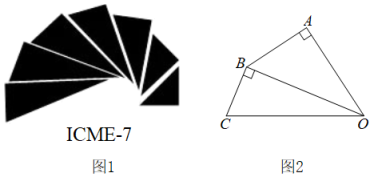 A、 B、 C、 D、1
A、 B、 C、 D、1 -
11. 如图,在矩形中, , , 点E、F分别为、的中点,、相交于点G,过点E作 , 交于点H,则线段的长度是( )
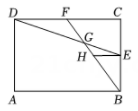 A、 B、1 C、 D、
A、 B、1 C、 D、 -
12. 中国人逢山开路,遇水架桥,靠自己勤劳的双手创造了世界奇迹.雅西高速是连接雅安和西昌的高速公路,被国内外专家学者公认为全世界自然环境最恶劣、工程难度最大、科技含量最高的山区高速公路之一,全长.一辆货车和一辆轿车先后从西昌出发驶向雅安,如图,线段表示货车离西昌距离与时间之间的函数关系:折线表示轿车离西昌距离与时间之间的函数关系,则以下结论错误的是( )
 A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km
A、货车出发1.8小时后与轿车相遇 B、货车从西昌到雅安的速度为 C、轿车从西昌到雅安的速度为 D、轿车到雅安20分钟后,货车离雅安还有20km
二、填空题
-
13. .
-
14. 盒子里装有除颜色外,没有其他区别的2个红球和2个黑球,搅匀后从中取出1个球,放回搅匀再取出第2个球,则两次取出的球是1红1黑的概率为.
-
15. 如果一元一次方程的解是一元一次不等式组的解.则称该一元一次方程为该一元一次不等式组的关联方程.若方程是关于x的不等式组的关联方程,则n的取值范围是 .
-
16. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当 , 且时,四边形是正方形.
其中正确结论有(填上所有正确结论的序号).

三、解答题
-
17. 解不等式: .
-
18. 同学们在探索“多边形的内角和”时,利用了“三角形的内角和”.请你在不直接运用结论“n边形的内角和为”计算的条件下,利用“一个三角形的内角和等于180°”,结合图形说明:五边形的内角和为540°.
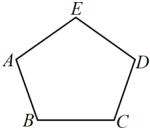
-
19. 为提高学生阅读兴趣,培养良好阅读习惯,2021年3月31日,教育部印发了《中小学生课外读物进校园管理办法》的通知.某学校根据通知精神,积极优化校园阅读环境,推动书香校园建设,开展了“爱读书、读好书、善读书”主题活动,随机抽取部分学生同时进行“你最喜欢的课外读物”(只能选一项)和“你每周课外阅读的时间”两项问卷调查,并绘制成如图1,图2的统计图.图1中A代表“喜欢人文类”的人数,B代表“喜欢社会类”的人数,C代表“喜欢科学类”的人数,D代表“喜欢艺术类”的人数.已知A为56人,且对应扇形圆心角的度数为126°.请你根据以上信息解答下列问题:
 (1)、在扇形统计图中,求出“喜欢科学类”的人数;(2)、补全条形统计图;(3)、该校共有学生3200人,估计每周课外阅读时间不低于3小时的人数.
(1)、在扇形统计图中,求出“喜欢科学类”的人数;(2)、补全条形统计图;(3)、该校共有学生3200人,估计每周课外阅读时间不低于3小时的人数. -
20. 如图,一次函数的图象与反比例函数的图象交于A、B两点,求的面积.
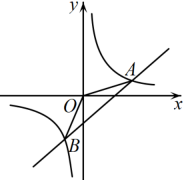
-
21. 如图,的直径垂直于弦于点F,点P在的延长线上,与相切于点C.
 (1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积.
(1)、求证:;(2)、若的直径为4,弦平分半径 , 求:图中阴影部分的面积. -
22. 第24届冬奥会(也称2022年北京冬奥会)于2022年2月4日至2月20日在中国北京举行,北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆,整个动作连贯一致,一气呵成,如图,某运动员穿着滑雪板,经过助滑后,从倾斜角的跳台A点以速度沿水平方向跳出,若忽略空气阻力影响,水平方向速度将保持不变.同时,由于受重力作用,运动员沿竖直方向会加速下落,因此,运动员在空中飞行的路线是抛物线的一部分,已知该运动员在B点着陆, , 且.忽略空气阻力,请回答下列问题:
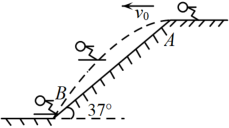 (1)、求该运动员从跳出到着陆垂直下降了多少m?(2)、以A为坐标原点建立直角坐标系,求该抛物线表达式;(3)、若该运动员在空中共飞行了4s,求他飞行2s后,垂直下降了多少m?
(1)、求该运动员从跳出到着陆垂直下降了多少m?(2)、以A为坐标原点建立直角坐标系,求该抛物线表达式;(3)、若该运动员在空中共飞行了4s,求他飞行2s后,垂直下降了多少m? -
23. 如图,二次函数的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为 , 点是其对称轴上一点,y轴上一点.
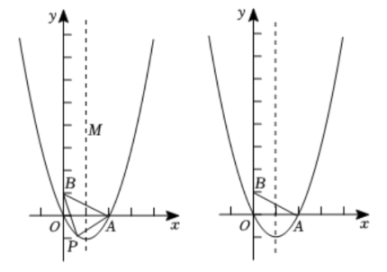 (1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.
(1)、求二次函数的表达式;(2)、二次函数在第四象限的图象上有一点P,连结 , , 设点P的横坐标为t,的面积为S,求S与t的函数关系式;(3)、在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由. -
24. 如图,直线分别与x轴、y轴交于点A、B,点C为线段上一动点(不与A、B重合),以C为顶点作 , 射线交线段于点D,将射线绕点O顺时针旋转交射线于点E,连接.
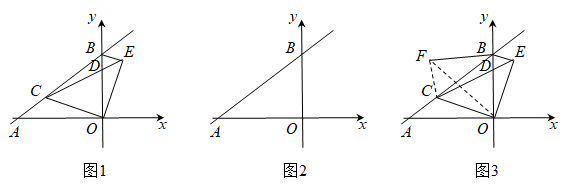 (1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)
(1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)
