2022-2023学年冀教版数学九年级上册期末模拟试卷2
试卷更新日期:2022-11-30 类型:期末考试
一、单选题(每题3分,共36分)
-
1. 为迎接建党一百周年,某班开展“我最想看的红色电影”投票活动,参选的五部电影的得票数分别是9,10,11,11,8,则这组得票数据的中位数,众数分别是( )A、10,11 B、11,10 C、11,11 D、10.5,112. 若一元二次方程的常数项是0,则的值是( )A、2或-2 B、2 C、-2 D、43. 已知点 , , 在反比例函数的图像上,则y1 ,y2的大小关系为( )A、 B、 C、 D、无法判断4. 如图: , , 那么CE的长为( )
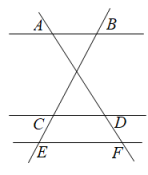 A、3 B、4 C、5 D、65. 如图,圆O的直径,弦 , 垂足为M,下列结论不成立的是( )
A、3 B、4 C、5 D、65. 如图,圆O的直径,弦 , 垂足为M,下列结论不成立的是( ) A、 B、 C、 D、6. 已知一元二次方程的两实数根分别为 , , 则的值为( )A、-2 B、2 C、 D、7. 如图,四边形ABCD是菱形,AC=8,tan∠DAC= ,DH⊥AB于H,则点D到AB边距离等于( )
A、 B、 C、 D、6. 已知一元二次方程的两实数根分别为 , , 则的值为( )A、-2 B、2 C、 D、7. 如图,四边形ABCD是菱形,AC=8,tan∠DAC= ,DH⊥AB于H,则点D到AB边距离等于( )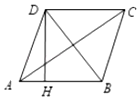 A、4 B、5 C、 D、8. 在同一平面直角坐标系中,一次函数与反比例函数的图象可能是( )A、
A、4 B、5 C、 D、8. 在同一平面直角坐标系中,一次函数与反比例函数的图象可能是( )A、 B、
B、 C、
C、 D、
D、 9. 如图,在中,:: , 是的中点,延长线交于 , 那么:( )
9. 如图,在中,:: , 是的中点,延长线交于 , 那么:( ) A、3:1 B、4:1 C、6:1 D、7:110. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、3(x﹣1)x=6210 B、3(x﹣1)=6210 C、(3x﹣1)x=6210 D、3x=621011. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )
A、3:1 B、4:1 C、6:1 D、7:110. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、3(x﹣1)x=6210 B、3(x﹣1)=6210 C、(3x﹣1)x=6210 D、3x=621011. 如图,菱形 中, , .以A为圆心, 长为半径画 ,点P为菱形内一点,连 , , .若 ,且 ,则图中阴影部分的面积为( )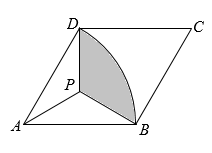 A、 B、 C、 D、12. 如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
A、 B、 C、 D、12. 如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )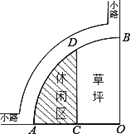
A、米2 B、米2 C、米2 D、米2二、填空题(每空3分,共18分)
-
13. 若一元二次方程有两个不相等的实数根 , , 且 , 则的值是 .14. 在中, , , 是BC上一点,把沿直线AE翻折后,点B落在点P处,如果 , 那么 .15. 已知一组数据:3,3,x,5,5的平均数是4,则 这组数据的方差是 .16. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口处立一根垂直于井口的木杆 , 从木杆的顶端观察井水水岸 , 视线与井口的直径交于点 , 如果测得米,米,米,那么井深为米.
 17. 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC于点E,若BD=6,AE=5,AB=7,则AC=.
17. 如图,⊙O是△ABC的外接圆,已知AD平分∠BAC交⊙O于点D,交BC于点E,若BD=6,AE=5,AB=7,则AC=. 18. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,点 是反比例函数 图象上一点, , 交 轴于点 , ,则 的值为 .
18. 如图,在平面直角坐标系中,点 , 的坐标分别为 , ,点 是反比例函数 图象上一点, , 交 轴于点 , ,则 的值为 .
三、解答题(共7题,共66分)
-
19. 已知关于的方程
①求证:方程有两个不相等的实数根.
②若方程的一个根是求另一个根及的值.
20. 如图,为了测量建筑物的高度,先从与建筑物的底部点水平相距100米的点处出发,沿斜坡行走至坡顶处,斜坡的坡度 , 坡顶到的距离米,在点处测得建筑物顶端点的仰角为 , 点在同一平面内,根据测量数据,请计算建筑物的高度(结果精确到1米).(参考数据:)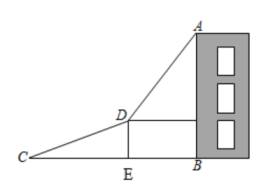 21. 如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.
21. 如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果点P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似. 22. 经销店为厂家代销一种新型环保水泥,当每吨售价为260元时,月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元.该经销店为扩大销售量、提高经营利润,计划采取降价的方式进行促销,经市场调查发现,当每吨售价每下降10元时,月销售量就会增加7.5吨.
22. 经销店为厂家代销一种新型环保水泥,当每吨售价为260元时,月销售量为45吨,每售出1吨这种水泥共需支付厂家费用和其他费用共100元.该经销店为扩大销售量、提高经营利润,计划采取降价的方式进行促销,经市场调查发现,当每吨售价每下降10元时,月销售量就会增加7.5吨.
(1)、填空:当每吨售价是240元时,此时的月销售量是吨.
(2)、该经销店计划月利润为9000元而且尽可能地扩大销售量,则售价应定为每吨多少元?23. 如图,Rt△ABO的顶点A是双曲线 与直线y=−x−(k+1)在第二象限的交点,AB⊥x轴于B且S△ABO= 。 (1)、求这两个函数的解析式。(2)、求直线与双曲线的两个交点A,C的坐标和△AOC的面积。24. 某销售部共有15名营销员.为了制定某种商品的月销售定额,随机抽取了这15名营销员一个月的销售量,统计结果如下表:
(1)、求这两个函数的解析式。(2)、求直线与双曲线的两个交点A,C的坐标和△AOC的面积。24. 某销售部共有15名营销员.为了制定某种商品的月销售定额,随机抽取了这15名营销员一个月的销售量,统计结果如下表:每人销售件数
1800
510
250
210
150
120
人数
1
1
3
5
3
2
(1)、写出这15位营销人员月销售量的中位数是 件、众数是 件;(2)、求这15位营销员该月销售量的平均数;(3)、你认为应从“平均数”、“中位数”两个统计量中选取哪一个作为月销售定额较为合适,说说你的理由.25. 已知的直径为10,D为上一动点(不与A、B重合),连接.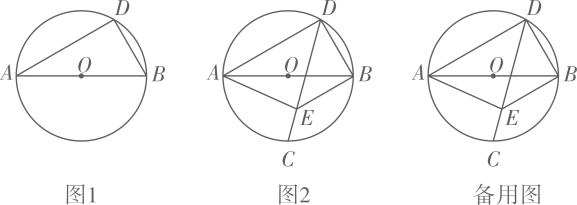 (1)、如图1,若 , 求的值;(2)、如图2,弦平分 , 过点A作于点E,连接.
(1)、如图1,若 , 求的值;(2)、如图2,弦平分 , 过点A作于点E,连接.①当时,求的值;
②在点D的运动过程中,的值是否存在最小值?若存在,求的最小值;若不存在,请说明理由.