2022-2023学年冀教版数学九年级上册期末模拟试卷1
试卷更新日期:2022-11-30 类型:期末考试
一、单选题(每题3分,共36分)
-
1. 若一元二次方程的常数项是0,则的值是( )A、2或-2 B、2 C、-2 D、42. 甲,乙,丙,丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是 , , , , 在本次射击测试中,这四个人成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁3. 两个相似三角形的对应边上的中线比为 , 则它们面积比的为( )A、 B、 C、 D、4. 若是一元二次方程的一个根,则的值是( )A、0 B、1 C、2 D、35. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )
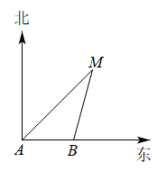 A、海里 B、海里 C、40海里 D、海里6. 反比例函数图象经过点、、 , 则a、b、c的大小关系是( )A、 B、 C、 D、7. 如图,已知点A,B,C依次在⊙o上,∠B-∠A=40°,则∠AOB的度数为( )
A、海里 B、海里 C、40海里 D、海里6. 反比例函数图象经过点、、 , 则a、b、c的大小关系是( )A、 B、 C、 D、7. 如图,已知点A,B,C依次在⊙o上,∠B-∠A=40°,则∠AOB的度数为( )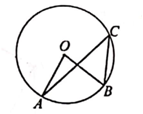 A、84° B、80° C、72° D、70°8. 班长王亮依据今年月“书香校园”活动中全班同学的课外阅读数量单位:本 , 绘制了如图折线统计图,下列说法正确的是( )
A、84° B、80° C、72° D、70°8. 班长王亮依据今年月“书香校园”活动中全班同学的课外阅读数量单位:本 , 绘制了如图折线统计图,下列说法正确的是( ) A、每月阅读数量的平均数是58 B、众数是83 C、中位数是50 D、每月阅读数量超过50的有5个月9. 已知a、b是一元二次方程x2-3x-1=0的两实数根,则=( )A、3 B、-3 C、 D、-10. 如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
A、每月阅读数量的平均数是58 B、众数是83 C、中位数是50 D、每月阅读数量超过50的有5个月9. 已知a、b是一元二次方程x2-3x-1=0的两实数根,则=( )A、3 B、-3 C、 D、-10. 如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )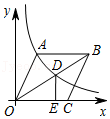 A、1 B、 C、2﹣ D、﹣111. 如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
A、1 B、 C、2﹣ D、﹣111. 如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:①AD2+AC2=4;②∠DBC+∠ADO=90°;③若AC=BD,则DE=OE;④若点P为BD的中点,则DE=2OE.
其中正确的是( )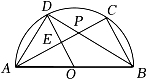 A、①②③ B、②③④ C、③④ D、②④12. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为 ,则下面所列方程正确的是( )
A、①②③ B、②③④ C、③④ D、②④12. 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 . 若设道路的宽为 ,则下面所列方程正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共18分)
-
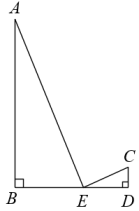
13. 计算:(﹣2016)0+|1﹣ |﹣2sin60°= .14. 一组数据4,4,5,5,x,6,7的平均数是5,则这组数据的中位数是.15. 如图所示,于点B,于点D, , 点E在上移动,当以为顶点的三角形与相似时,求的长为 .
 16. 2021年,某市准备加大对雾霾的治理力度,2021年第一季度投入资金100万元,第二季度和第三季度计划共投入资金260万元. 设这两个季度计划投入资金的平均增长率为x,则列方程是17. 如图,反比例函数在第一象限的图象上有A(1,6),B(3,b)两点,直线与x轴相交于点C,D是线段上一点.若 , 连接 , 记 , 的面积分别为 , , 则的值为 .
16. 2021年,某市准备加大对雾霾的治理力度,2021年第一季度投入资金100万元,第二季度和第三季度计划共投入资金260万元. 设这两个季度计划投入资金的平均增长率为x,则列方程是17. 如图,反比例函数在第一象限的图象上有A(1,6),B(3,b)两点,直线与x轴相交于点C,D是线段上一点.若 , 连接 , 记 , 的面积分别为 , , 则的值为 .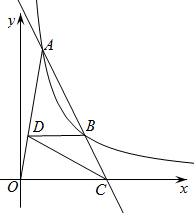 18. 如图,正方形 中,E为 上一点, 于点F,已知 ,过C、D、F的 与边 交于点G,则 .
18. 如图,正方形 中,E为 上一点, 于点F,已知 ,过C、D、F的 与边 交于点G,则 .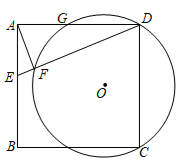
三、解答题(共6题,共66分)
-
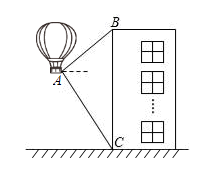
19. 关于 的一元二次方程 有两个不等实根 , .(1)、求实数 的取值范围;(2)、若方程两实根 , 满足 ,求 的值。20. 某学校升气球庆祝党的二十大胜利召开.如图,一气球到达离地面高度为12米的处时,仪器显示正前方一高楼顶部的仰角是 , 底部的俯角是 . 气球要飞到楼顶,应至少再上升多少米?(结果精确到0.1米)(参考数据: , , , )
 21. 有甲、乙两家肉禽类公司到某超市推销鸡腿,两家鸡腿价格相同,品质相似.超市决定通过评估质量来确定选择哪家鸡腿,检查人员从两家分别抽取了100个鸡腿,然后再从中随机各抽取20个,这些鸡腿的质量记为x(单位:克),将所得的数据分为5组(A组: , 组, , 组: , 组: , 组:),学校对数据进行分析后,得到如下部分信息:
21. 有甲、乙两家肉禽类公司到某超市推销鸡腿,两家鸡腿价格相同,品质相似.超市决定通过评估质量来确定选择哪家鸡腿,检查人员从两家分别抽取了100个鸡腿,然后再从中随机各抽取20个,这些鸡腿的质量记为x(单位:克),将所得的数据分为5组(A组: , 组, , 组: , 组: , 组:),学校对数据进行分析后,得到如下部分信息:甲公司被抽取的20个鸡腿质量频数分布直方图(图1):
乙公司被抽取的20个鸡腿质量扇形统计图(图2):
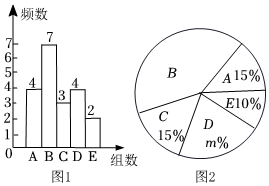
甲公司被抽取的鸡腿质量在这一组的数据是:75,76,78,76,77,78,79.
乙公司被抽取的鸡腿质量在这一组的数据是:75,78,75,75,75,77,76,75.
甲、乙公司被抽取的鸡腿质量的平均数、中位数、众数如下:
公司
甲公司
乙公司
平均数
73
73
中位数
n 75
众数
74
根据以上信息,解答下列问题:
(1)、直接写出上述表中 , , ;(2)、根据以上数据,请估算乙公司这100个鸡腿中质量不低于75克的数量;(3)、根据以上数据分析,如果你是超市采购人员,你会选择采购哪个公司的鸡腿,请说明理由(写出一条理由即可).22. 如图,是的直径,点 , 是上的点,且 , 分别与 , 相交于点 , .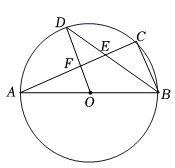 (1)、求证:点为的中点;(2)、若 , , 求的直径.23. 某服装店在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件.现服装店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件.(1)、求销售价在每件90元的基础上,每件降价多少元时,平均每天销售这种服装能盈利1200元,同时又要使顾客得到较多的实惠?(2)、要想平均每天盈利2000元,可能吗?请说明理由.24. 如图,直线与双曲线在第一象限内交于两点,已知 .
(1)、求证:点为的中点;(2)、若 , , 求的直径.23. 某服装店在销售中发现:进货价为每件50元,销售价为每件90元的某品牌服装平均每天可售出20件.现服装店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每件服装降价1元,那么平均每天就可多售出2件.(1)、求销售价在每件90元的基础上,每件降价多少元时,平均每天销售这种服装能盈利1200元,同时又要使顾客得到较多的实惠?(2)、要想平均每天盈利2000元,可能吗?请说明理由.24. 如图,直线与双曲线在第一象限内交于两点,已知 .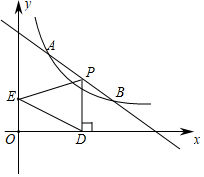 (1)、求的值及直线的解析式.(2)、根据函数图象,直接写出不等式的解集.(3)、设点是线段上的一个动点,过点作轴于点是轴上一点,当的面积为时,请直接写出此时点的坐标.
(1)、求的值及直线的解析式.(2)、根据函数图象,直接写出不等式的解集.(3)、设点是线段上的一个动点,过点作轴于点是轴上一点,当的面积为时,请直接写出此时点的坐标.