浙教版备考2023年中考数学一轮复习13.二次根式及其运算
试卷更新日期:2022-11-28 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 下列式子不是二次根式的是( )A、 B、 C、 D、
-
2. 下列计算不正确的是( )A、 B、 C、 D、
-
3. 下列二次根式中,可与合并的是( )A、 B、 C、 D、
-
4. 要使分式有意义,的取值范围是( )A、 B、 C、 D、
-
5. 估计的值应在( )A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间
-
6. 我们知道的小数部分b为 , 如果用a代表它的整数部分,那么的值是( )A、8 B、-8 C、4 D、-4
-
7. 观察下列各式: , ……, , ……请你从上述等式中找出规律,并利用这一规律计算:的值是( )A、 B、 C、 D、
-
8. 已知数a,b,c在数轴上的位置如图所示,化简:的结果是( )
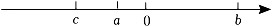 A、2c-2b B、-2c C、-2a-2c D、0
A、2c-2b B、-2c C、-2a-2c D、0 -
9. 对于任意的正数m、n定义运算※为:m※n= , 计算(3※2)×(8※12)的结果为( )A、2﹣4 B、2 C、2 D、20
-
10. 我国宋代数学家秦九韶和古希腊几何学家海伦都曾提出利用三角形的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是a,b,c,记 ,那么三角形的面积为 .如图,在 中, , , 所对的边分别记为a,b,c,若 , , ,则 的面积为( )
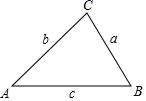 A、 B、 C、24 D、
A、 B、 C、24 D、
二、填空题(每题3分,共18分)
-
11. 与最简二次根式可以合并,则 .
-
12. 已知 的小数部分是a,则 的值是.
-
13. 已知 , , 则的值是.
-
14. 已知x,y均为实数,y= , 则x+y的值为
-
15. 化简题中,有四个同学的解法如下:
①
②
③
④
他们的解法,正确的是 . (填序号)
-
16. 如图,一个长方形被分割成四部分,其中图形①,②,③都是正方形,且正方形①,③的面积分别为16和3,则图中阴影部分的面积为 .

三、计算题(共8分)
-
17. 计算:(1)、÷-×+;(2)、--( -2);(3)、(2-)2017×(2+)2016-2-(-)0(4)、(a+2+b)÷(+)-(-).
四、解答题(共8题,共64分)
-
18. 已知 ,求 的值.
-
19. 设矩形的面积为S,相邻两边长分别为a、b,对角线长为l,已知S=2 , b= , 求a和l.
-
20. 已知 , , 分别求下列代数式的值:(1)、(2)、
-
21. 在解决问题“已知a= ,求3a2﹣6a﹣1的值”时,小明是这样解答的:
∵a= ,
∴a﹣1= ,
∴(a﹣1)2=2,即a2﹣2a+1=2,
∴a2﹣2a=1,
∴3a2﹣6a=3,
∴3a2﹣6a﹣1=2.
请你根据小明的解答过程,解决下面的问题:
若a= ,求2a2﹣12a+1的值.
-
22. 高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度h(单位:m)近似满足公式t= (不考虑风速的影响).(1)、从50m高空抛物到落地所需时间t1是多少s,从100m高空抛物到落地所需时间t2是多少s;(2)、t2是t1的多少倍?(3)、经过1.5s,高空抛物下落的高度是多少?
-
23. 先阅读下列的解答过程,然后再解答:
形如的化简,只要我们找到两个正数 , 使 , , 使得 , , 那么便有:().
例如:化简
解:首先把化为 , 这里 , 由于 ,
即 , ,
∴ .
(1)、根据以上例子,请填空 =; =;(2)、化简, -
24. 阅读下面问题:
;
;
.
试求:
(1)、 的值;(2)、 的值;(3)、 为正整数 的值. -
25. 我们将 , 称为一对“对偶式”.因为 =a-b.所以构造“对偶式”再将其相乘可以有效地将 和 中的“ ”去掉.例如: 。像这样,通过分子、分母同乘以一个式子把分母中的根号化去,叫做分母有理化.
根据以上材料,理解并运用材料提供的方法,解答以下问题.
(1)、分母有理化 的值为;(2)、计算:
