高中数学人教A版（2019）必修一第五章第六节 y=Asin(wx+φ )

试卷更新日期：2022-11-28 类型：同步测试

进入出卷网下载

一、单选题

1. 函数 $f (x) = A s i n (ω x + φ) (| φ | < π)$ 的部分图象如图所示，则下列结论错误的是（）．

A、频率为 $\frac{1}{6}$ B、周期为6π C、振幅为2 D、初相为 $- \frac{π}{6}$

查看试题解析
2. 为了得到函数 $y = s i n 2 x$ 的图象，可将函数 $y = s i n (2 x - \frac{π}{3})$ 图象上的所有点（）

A、向右平移 $\frac{π}{3}$ 个单位 B、向左平移 $\frac{π}{3}$ 个单位 C、向右平移 $\frac{π}{6}$ 个单位 D、向左平移 $\frac{π}{6}$ 个单位

查看试题解析
3. 已知函数 $f (x) = s i n (2 x - \frac{π}{4})$ ， $g (x) = c o s (2 x + \frac{π}{4})$ ，下列说法正确的是（）

A、曲线 $y = f (x)$ 向左平移 $\frac{π}{4}$ 个单位长度得到曲线 $y = g (x)$ B、曲线 $y = f (x)$ 向右平移 $\frac{π}{4}$ 个单位长度得到曲线 $y = g (x)$ C、曲线 $y = f (x)$ 与曲线 $y = g (x)$ 关于 $y$ 轴对称 D、曲线 $y = f (x)$ 与曲线 $y = g (x)$ 关于 $x$ 轴对称

查看试题解析
4. 若函数 $f (x) = s i n (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的图象（部分）如图所示，则 $f (x)$ 的解析式为（）

A、 $f (x) = s i n (\frac{1}{2} x + \frac{π}{6})$ B、 $f (x) = s i n (2 x + \frac{π}{3})$ C、 $f (x) = s i n (\frac{1}{2} x + \frac{π}{3})$ D、 $f (x) = s i n (2 x + \frac{π}{6})$

查看试题解析
5. 把函数 $y = s i n x (x \in R)$ 的图象上所有点向左平行移动 $\frac{π}{3}$ 个单位长度，再把所得图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ 倍（纵坐标不变），得到的图象所表示的函数是（）

A、 $y = s i n (2 x - \frac{π}{3})$ ， $x \in R$ B、 $y = s i n (\frac{x}{2} + \frac{π}{6})$ ， $x \in R$ C、 $y = s i n (\frac{x}{2} + \frac{2 π}{3})$ ， $x \in R$ D、 $y = s i n (2 x + \frac{π}{3})$ ， $x \in R$

查看试题解析
6. 为了得到函数 $y = 3 s i n (2 x + \frac{π}{5})$ 的图象，只要把函数 $y = 3 s i n (x + \frac{π}{5})$ 图象上所有的点（）

A、横坐标伸长到原来的2倍，纵坐标不变 B、横坐标缩短到原来的 $\frac{1}{2}$ 倍，纵坐标不变 C、纵坐标伸长到原来的2倍，横坐标不变 D、纵坐标缩短到原来的 $\frac{1}{2}$ 倍，横坐标不变

查看试题解析
7. 为了得到函数 $y = s i n (2 x - \frac{π}{4})$ 的图象，只需把函数 $y = c o s 2 x$ 的图象上所有点（）

A、向左平移 $\frac{π}{4}$ 个单位长度 B、向右平移 $\frac{π}{4}$ 个单位长度 C、向左平移 $\frac{3 π}{8}$ 个单位长度 D、向右平移 $\frac{3 π}{8}$ 个单位长度

查看试题解析
8. 要得到 $y = c o s (2 x - \frac{π}{3})$ 的图像，只需将函数 $y = s i n 2 x$ 的图像（）

A、向左平移 $\frac{π}{12}$ 个单位 B、向右平移 $\frac{π}{12}$ 个单位 C、向左平移 $\frac{π}{6}$ 个单位 D、向右平移 $\frac{π}{6}$ 个单位

查看试题解析

二、多选题

9. 函数 $y = A s i n (ω x + φ) (A > 0 ， ω > 0 ， 0 < φ < π)$ 在一个周期内的图象如图所示，则（）．

A、该函数的解析式为 $y = 2 s i n (\frac{2}{3} x + \frac{π}{3})$ B、该函数图象的对称中心为 $(k π - \frac{π}{3} ， 0)$ ， $k ∈ Z$ C、该函数的单调递增区间是 $(3 k π - \frac{5 π}{4} ， 3 k π + \frac{π}{4})$ ， $k ∈ Z$ D、把函数 $y = 2 s i n (x + \frac{π}{3})$ 的图象上所有点的横坐标伸长为原来的 $\frac{3}{2}$ 倍，纵坐标不变，可得到该函数图象

查看试题解析
10. 函数 $f (x) = A s i n (ω x + φ) (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示，将 $f (x)$ 的图象上所有点的横坐标扩大到原来的4倍（纵坐标不变），再把所得的图象沿x轴向左平移 $\frac{π}{3}$ 个单位长度，得到函数 $g (x)$ 的图象，则对函数 $g (x)$ 的描述正确的是（）

A、 $[- \frac{5 π}{3} ， \frac{π}{3}]$ 为函数 $g (x)$ 的一个递增区间 B、 $x = \frac{π}{3}$ 为函数 $g (x)$ 的一条对称轴 C、 $(\frac{4 π}{3} ， 0)$ 为函数 $g (x)$ 的一个对称点 D、函数 $g (x)$ 的最小正周期为 $T = 4 π$

查看试题解析
11. 已知函数 $f (x) = A c o s (ω x + φ) (A > 0 ， ω > 0 ， 0 < φ < π)$ 的部分图象如图所示，则下列说法正确的是（）

A、 $f (x) = 2 c o s (2 x + \frac{π}{3})$ B、函数 $f (x)$ 的图象关于点 $(\frac{π}{6} ， 0)$ 对称 C、 $\forall x \in R$ ， $f (x) = f (\frac{5 π}{6} - x)$ D、函数 $f (x)$ 在 $(0 ， \frac{π}{2})$ 上无最小值

查看试题解析
12. 若将函数 $f (x) = c o s (2 x + \frac{π}{12})$ 的图象向左平移 $\frac{π}{8}$ 个单位长度，得到函数 $g (x)$ 的图象，则下列说法正确的是（）

A、 $g (x)$ 的最小正周期为 $π$ B、 $g (x)$ 在区间 $[0 ， \frac{π}{2}]$ 上单调递减 C、 $x = \frac{π}{12}$ 不是函数 $g (x)$ 图象的对称轴 D、 $g (x)$ 的图象关于点 $(- \frac{5 π}{12} ， 0)$ 对称

查看试题解析

三、填空题

13. 已知函数 $f (x) = 2 s i n (x + \frac{π}{6})$ ，将函数图象上各点的横坐标缩短到原来的 $\frac{1}{2}$ 倍(纵坐标不变)，再将得到的图象向右平移 $\frac{π}{4}$ 个单位，得到函数的解析式．

查看试题解析
14. 若函数 $y = 3 s i n (ω x + φ) (ω > 0 ， 0 \leq φ < 2 π)$ 的部分图象如图所示，则此函数的解析式为.

查看试题解析
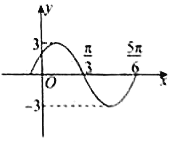15. 将函数 $y = s i n (2 x + \frac{π}{12})$ 图象上的所有点向右平行移动 $\frac{π}{12}$ 个单位长度，则所得图象的函数解析式为.

查看试题解析
16. 若将函数 $y = c o s x - \sqrt{3} s i n x$ 的图像向左平移 $m (m > 0)$ 个单位后所得图像关于 $y$ 轴对称，则 $m$ 的最小值为.

查看试题解析

四、解答题

17. 已知函数 $f (x) = 2 s i n x (s i n x + c o s x) + a$ 的最大值为 $\sqrt{2}$ .

(1)、求 $f (x)$ 的最小正周期以及实数 $a$ 的值；

(2)、将函数 $y = f (x)$ 的图象向左平移 $\frac{π}{4}$ 个单位，得到函数 $y = g (x)$ 的图象，若 $f (θ) + g (θ) = \frac{8}{5}$ ，求 $t a n θ$ 的值.

查看试题解析
18. 已知函数 $f (x) = 2 s i n^{2} x + c o s (2 x - \frac{π}{3}) - 1$ ．

(1)、求 $f (x)$ 的单调递增区间；

(2)、将函数 $f (x)$ 的图象向左平移 $m (m > 0)$ 个单位长度，所得函数图象与函数 $y = c o s (2 x + \frac{π}{3})$ 的图象重合，求实数m的最小值．

查看试题解析
19. 已知函数 $f (x) = s i n 2 ω x + \sqrt{3} c o s 2 ω x (ω > 0)$ ，该函数图象一条对称轴与其相邻的一个对称中心的距离为 $\frac{π}{4}$ ．

(1)、求函数 $f (x)$ 的对称轴和对称中心；

(2)、求 $f (x)$ 在 $[- \frac{π}{4} ， \frac{3 π}{4}]$ 上的单调递增区间．

查看试题解析
20. 如图是函数 $f (x) = A s i n (ω x + φ) (A > 0 ， ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象.

(1)、求函数 $f (x)$ 的解析式；

(2)、若 $c o s^{4} α - s i n^{4} α = \frac{4}{5}$ ， $α \in (0 ， \frac{π}{2})$ ，求 $f (α)$ .

查看试题解析
21. 已知函数 $f (x) = 2 \sqrt{3} s i n x c o s x + 2 c o s^{2} x$ .

(1)、求函数 $f (x)$ 的周期和单调递减区间；

(2)、将 $f (x)$ 的图象向右平移 $\frac{π}{6}$ 个单位，得到 $g (x)$ 的图象，已知 $g (x_{0}) = \frac{23}{13}$ ， $x_{0} \in [\frac{π}{3} ， \frac{π}{2}]$ ，求 $c o s 2 x_{0}$ 值.

查看试题解析
22. 已知函数 $f (x) = 2 s i n x c o s x + 2 \sqrt{3} c o s^{2} x - \sqrt{3}$

(1)、求函数 $f (x)$ 的最小正周期和单调递减区间；

(2)、将函数 $f (x)$ 的图像向左平移 $\frac{π}{6}$ 单位长度，再将所得图像上各点的横坐标缩短为原来的 $\frac{1}{2}$ ，纵坐标不变，得到函数的 $g (x)$ 图像，求 $y = g (x)$ 在 $(- \frac{π}{12} ， \frac{π}{8})$ 上的值域．

查看试题解析
23. 已知函数 $f (x) = s i n (π - ω x) c o s ω x - c o s^{2} (ω x + \frac{π}{4}) (ω > 0)$ 的最小正周期为 $π$ ．

(1)、求 $f (x)$ 图象的对称轴方程；

(2)、将 $f (x)$ 的图象向左平移 $\frac{π}{6}$ 个单位长度后，得到函数 $g (x)$ 的图象，求函数 $g (x)$ 在 $[0 ， \frac{π}{2}]$ 上的值域．

查看试题解析
24. 已知函数 $f (x) = 2 s i n (ω x + φ)$ $(ω > 0 ， 0 < φ < π)$ 在一个周期内的图象如图所示．

(1)、求 $f (x)$ 的解析式；

(2)、直接写出 $f (x)$ 在区间 $[0 ， π]$ 上的单调区间；

(3)、已知 $\forall x \in R$ ， $f (a - x) = f (a + x)$ 都成立，直接写出一个满足题意的 $a$ 值．

查看试题解析

高中数学人教A版（2019）必修一 第五章 第六节 y=Asin(wx+φ )

一、单选题

二、多选题

三、填空题

四、解答题

高中数学人教A版（2019）必修一第五章第六节 y=Asin(wx+φ )