广西壮族自治区南宁市教育局教学研究室2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-11-28 类型：期中考试

进入出卷网下载

一、单选题

1. -2的相反数是（）

A、 $- \frac{1}{2}$ B、 $- 2$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 下列各数中，最小的数是（）

A、－3 B、0 C、1 D、2

查看试题解析
3. 2022年2月4日，第24届冬奥会在北京开幕，在中国大陆地区观看开幕式的人数约为 $316000000$ 人，其中数据“ $316000000$ ”用科学记数法表示为（）

A、 $31.6 \times 1 0^{7}$ B、 $31.6 \times 1 0^{8}$ C、 $3.16 \times 1 0^{8}$ D、 $3.16 \times 1 0^{9}$

查看试题解析
4. 一天早晨的气温是 $- 7 ℃$ ，中午上升了 $11 ℃$ ，这天中午的气温是（）

A、 $- 18 ℃$ B、 $18 ℃$ C、 $- 4 ℃$ D、 $4 ℃$

查看试题解析
5. 下列运算正确的是（）

A、 $4 a + b = 4 a b$ B、 $a^{2} + a^{3} = a^{5}$ C、 $3 a + 2 a = 5 a$ D、 $2 a^{2} b^{3} - 2 a^{3} b^{2} = 0$

查看试题解析
6. 若单项式 $- 2 x^{m} y^{n}$ 与 $6 x^{3} y^{2}$ 是同类项，则 $m ， n$ 分别是（）

A、 $m = 3 ， n = 2$ B、 $m = 2 ， n = 3$ C、 $m = - 2 ， n = - 3$ D、 $m = - 2 ， n = 3$

查看试题解析
7. 下列说法不正确的是（）

A、0既不是正数，也不是负数 B、1是绝对值最小的正数 C、整数和分数统称有理数 D、圆周率兀精确到百分位约是3.14

查看试题解析
8. 如图是一个简单的数值运算程序，当输入的值为 $- 3$ 时，输出的值为（）

A、6 B、-6 C、4 D、-4

查看试题解析
9. 有理数 $a ， b$ 在数轴上对应的点的位置如图所示，则下列结论正确的是（）

A、 $a > 0$ B、 $b < 1$ C、 $a + 1 > 0$ D、 $a - b > 0$

查看试题解析
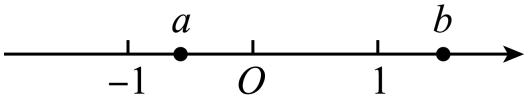10. 若 $| x | = 3$ ， $| y | = 2$ ，且 $x y > 0$ ，则 $x + y$ 的值是（）

A、5 B、±5 C、6 D、±6

查看试题解析
11. 中国古代《孙子算经》中有个问题：今天有四人共车，一车空；二人共车，八人步.问人与车各几何？这道题的意思是：今有若干人乘车，每4人乘一车，恰好剩余1辆车无人坐；若每2人共乘一车，最终剩余8个人无车可乘，问有多少人？多少辆车？如果设有x辆车.则总人数可表示为（）

A、 $4 (x - 1)$ B、 $4 (x + 1)$ C、 $2 x - 8$ D、 $2 (x + 1) - 8$

查看试题解析
12. 观察下列图形，则第2022个图形中三角形的个数是（）

A、8084 B、8088 C、2021 D、2022

查看试题解析

二、填空题

13. 计算： $- 5 + 4 =$ .

查看试题解析
14. 对式子“ $3 x$ ”，可以这样解释：苹果每千克 $3$ 元，某人买了 $x$ 千克，共付 $3 x$ 元．请你再对“ $3 x$ ”给出另一个实际生活方面的合理解释：．

查看试题解析
15. 若 $a 、 b$ 互为相反数， $c 、 d$ 互为倒数，则 $\frac{1}{c d} - a - b =$ .

查看试题解析
16. 规定一种新运算“★”对于任意两个有理数a和b，有 $a ★ b = a - b \times 2$ ，请你根据新运算，计算 $2 ★ (- 3)$ 的值是.

查看试题解析
17. 若多项式xy^|m^-n^|+（n-1）x²y²+1是关于x，y的三次多项式，则mn＝.

查看试题解析
18. 如图，把五个长为b、宽为 $a (b > a)$ 的小长方形，按图1和图2两种方式放在一个宽为 $m$ 的大长方形上（相邻的小长方形既无重叠，又不留空隙）.设图1中两块阴影部分的周长和为 $C_{1}$ ，图2中阴影部分的周长为 $C_{2}$ ，若大长方形的长比宽大 $（ 6 - a ）$ ，则 $C_{2} - C_{1}$ 的值为.

查看试题解析

三、解答题

19. 计算： $- 1^{2} \times 3 + (1 - 3) \div 4$ .

查看试题解析
20. 先化简，后求值： $(- 2 a b + 3 a) - 2 (2 a - b ） + 2 a b$ ，其中a=3，b=1.

查看试题解析
21.

(1)、画出数轴，把下列各数 $0 ， - (- 3) ， {(- 1)}^{2} ， - | - 2 | ， - 1$ 在数轴上表示出来.

(2)、将上列各数用“<”连接起来.

查看试题解析
22. 入冬以来，某品牌的羽绒服统计了在西乡市场某一周的销售情况，以每天100件为标准，超过的件数记作正数，不足的件数记作负数，记录如下：8，12， $- 9$ ， 6， $- 11$ ， 10， $- 2$ .

(1)、求销量最多的一天比销量最少的一天多销售多少件？

(2)、该品牌羽绒服这一周的销售总量是多少件？

(3)、若每件羽绒服的利润为130元，则这一周销售该品牌羽绒服的总利润为多少元？

查看试题解析
23. 阅读理解：整体代换是一种重要的数学思想方法.例如：计算 $2 (2 m + n) - 5 (2 m + n) + (2 m + n)$ 时，可将(2m+n)看成一个整体，合并同类项得 $- 2 (2 m + n)$ ，再利用分配律去括号得 $- 4 m - 2 n$ .

(1)、若已知 $2 m + n = 3$ ，请你利用整体代换思想求代数式 $8 m + 4 n - 12$ 的值；

(2)、某同学做一道题，已知两个多项式A、B，求 $A - B$ 的值.他误将“ $A - B$ ”看成“ $A + B$ ”，经过正确计算得到的结果是 $2 x^{2} + 14 x - 6$ .已知： $A = x^{2} + 7 x - 1$ ，请你帮助这位同学求出 $A - B$ 正确的值.

查看试题解析
24. 如图，希望中学要在校园内两块紧挨在一起的长方形荒地上修建一个半圆形花圃，尺寸如图所示（单位：米）

(1)、求阴影部分的面积（用含x的代数式表示）；

(2)、当 $x = 7$ 时，求阴影部分的面积（结果保留 $π$ ）.

查看试题解析
25. 运算律是解决许多数学问题的基础，在运算中有重要的作用，充分运用运算律能使计算简便高效.
例如： $(- 125 \frac{5}{7}) ÷ (- 5)$ .

解： $(- 125 \frac{5}{7}) \div (- 5) = 125 \frac{5}{7} \times \frac{1}{5} = (125 + \frac{5}{7}) \times \frac{1}{5} = 125 \times \frac{1}{5} + \frac{5}{7} \times \frac{1}{5} = 25 + \frac{1}{7} = 25 \frac{1}{7}$ .

(1)、计算： $(- \frac{3}{2} - \frac{2}{3}) \div \frac{1}{6}$ ， A同学的计算过程如下：
原式 $= (- \frac{3}{2} - \frac{2}{3}) \times 6 = (- \frac{3}{2}) \times 6 + \frac{2}{3} \times 6 = - 9 + 4 = - 5$ .
请你判断A同学的计算过程是否正确，若不正确，请你写出正确的计算过程.

(2)、请你参考例题，用运算律简便计算（请写出具体的解题过程）： $999 \times 118 \frac{4}{5} + 333 \times (- \frac{3}{5}) - 999 \times 118 \frac{3}{5}$ .

查看试题解析
26. 已知点M在数轴上对应的数为a，点N在数轴上对应的数为b，M、N之间的距离记为 $| M N | = | a - b | 或 | b - a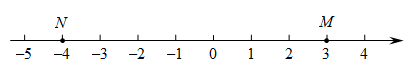 |$ ，请回答下列问题：

(1)、如图：当 $a = 3 ， b = - 4$ 时， $| M N | =$ ；

(2)、在（1）的条件下，动点P表示的数为y，若点P在点M，N之间，则 $| y - 3 | + | y + 4 | =$ ；

(3)、在（1）的条件下，若点P表示的数是-8，现有一虫子从点P出发，以每秒1个单位长度的速度向右运动，当经过多少秒时，虫子所在的点到点M，点N的距离之和是10？

查看试题解析