广西壮族自治区南宁市教育局教学研究室2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-11-28 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四幅图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在 $Δ A B C$ 中，若 $∠ A = 60 ° ， ∠ B = 40 °$ ，则 $∠ C$ 的度数为（）

A、 $40 °$ B、 $60 °$ C、 $80 °$ D、 $100 °$

查看试题解析
3. 在下列长度的三条线段中，能围成三角形的是（）

A、2，3，4 B、2，3，5 C、3，5，9 D、8，4，4

查看试题解析
4. 如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝3cm，则线段PB的长为（　　）

A、6cm B、5cm C、4cm D、3cm

查看试题解析
5. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（　　）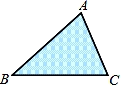

A、△ABC 的三条中线的交点 B、△ABC 三边的垂直平分线的交点 C、△ABC 三条角平分线的交点 D、△ABC 三条高所在直线的交点

查看试题解析
6. 如图，一块玻璃被打碎成三块，如果要去玻璃店配一块完全一样的玻璃，那么最合理的办法是（）

A、带①去 B、带②去 C、带③去 D、带①②③去

查看试题解析
7. 若点 $A (m ， - 2)$ ， $B (- 4 ， n - 3)$ 关于x轴对称，则（）

A、 $m = - 4$ ， $n = 5$ B、 $m = - 4$ ， $n = - 5$ C、 $m = 4$ ， $n = 1$ D、 $m = 4$ ， $n = - 1$

查看试题解析
8. 工人师傅常用角尺平分一个任意角，具体做法如下：如图，已知 $∠ A O B$ 是一个任意角，在边 $O A ， O B$ 上分别取 $O M = O N$ ，移动角尺，使角尺两边相同的刻度分别与点 $M ， N$ 重合，则过角尺顶点C的射线 $O C$ 便是 $∠ A O B$ 的平分线 $．$ 在证明 $△ M O C ≌ △ N O C$ 时运用的判定定理是（　　）

A、SSS B、SAS C、ASA D、AAS

查看试题解析
9. “三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角，这个三等分角仪由两根有槽的棒 $O A$ ， $O B$ 组成，两根棒在 $O$ 点相连并可绕 $O$ 转动， $C$ 点固定， $O C = C D = D E$ ，点 $D$ ， $E$ 可在槽中滑动，若 $∠ B D E = 75 °$ ，则 $∠ O$ 的度数是（）

A、 $15 °$ B、 $20 °$ C、 $25 °$ D、 $30 °$

查看试题解析
10. 如图所示，在△ABC中，∠C=90°，AD平分∠BAC ， DE⊥AB于E ， DE=4，BC=9，则BD的长为（）

A、6 B、5 C、4 D、3

查看试题解析
11. 如图，在 $△ A B C$ 中，已知点D、E、F分别为 $B C 、 A D 、 E C$ 的中点，且 $S_{△ A B C} = 8$ ，则阴影部分面积S是（）

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D$ 、 $C E$ 是 $△ A B C$ 的两条中线， $C E = 5 ， A D = 7$ ， P是 $A D$ 上一个动点，则 $B P + E P$ 的最小值是（）

A、7 B、3.5 C、5 D、2.5

查看试题解析

二、填空题

13. 如图，为了使木门不变形，木工师傅在木门上加钉了一根木条，这样是利用三角形的.

查看试题解析
14. 已知等腰三角形的一边长等于4，一边长等于8，则它的周长为.

查看试题解析
15. 如图，在网格图中选择一个格子涂阴影，使得整个图形是以虚线为对称轴的轴对称图形，则把阴影涂在图中标有数字的格子内．

查看试题解析
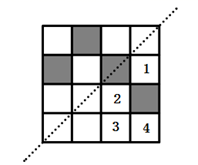16. 如图， $A B ⊥ B C ， A D ⊥ D C$ ，请你添加一个条件，利用“ $H L$ ”，证明 $R t △ A B C ≌ R t △ A D C$ .

查看试题解析
17. 如图，在 $△ A B C ≌ △ E D C$ ，点D落在 $A B$ 上，且 $∠ B = 60 °$ ，则 $∠ E D A =$ .

查看试题解析
18. 如图，已知 $∠ M O N = 30 °$ ，点 $A_{1} ， A_{2} ， A_{3}$ ……在射线 $O N$ 上，点 $B_{1} ， B_{2} ， B_{3}$ ……在射线 $O M$ 上， $△ A_{1} B_{1} A_{2} ， △ A_{2} B_{2} A_{3} ， △ A_{3} B_{3} A_{4}$ ……均为等边三角形，若 $O A_{1} = 3$ ，则 $△ A_{10} B_{10} A_{11}$ 的边长为.

查看试题解析

三、解答题

19. 计算： ${(- 1)}^{2} \times 3 + 4 \div (- 2)$ .

查看试题解析
20. 解不等式组 ${\begin{cases} 2 - x > 0 ① \\ \frac{5 x + 1}{2} + 1 \geq \frac{2 x - 1}{3} \end{cases} \begin{array}{l} ② \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
21. 如图，在平面直角坐标系中， $A (2 ， 4) ， B (3 ， 1) ， C (- 2 ， - 1)$ .

(1)、在图中作出 $△ A B C$ 关于x轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、写出点 $A_{1} 、 B_{1} 、 C_{1}$ 三点的坐标；

(3)、求 $△ A B C$ 的面积.

查看试题解析
22. 将正六边形与正五边形按如图所示方式摆放，公共顶点为O，且正六边形的边AB与正五边形的边DE在同一条直线上.

(1)、请求出∠ABO度数

(2)、请求出∠BOE的度数

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B = 30 °$ .

(1)、作线段 $A B$ 的垂直平分线 $M N$ 交 $B C$ 于D（保留作图痕迹）.

(2)、求证： $C D = 2 B D$ .

查看试题解析
24. 王强同学用10块高度都是 $2 c m$ 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（ $A C ＝ B C$ ， $∠ A C B ＝ 90 °$ ），点C在 $D E$ 上，点A和B分别与木墙的顶端重合.

(1)、求证： $∠ A C D = ∠ C B E$ ；

(2)、求两堵木墙之间的距离.

查看试题解析
25. 上数学活动课时，欢欢为测量池塘两端A、B的距离，设计了如下方案：

（1）如图1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC＝AC，EC＝BC，最后测出DE的距离即为AB的长；
（2）如图2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC＝CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离.

阅读后回答下列问题：

(1)、方案（1）是否可行？请说明理由.

(2)、方案（2）是否可行？请说明理由.

(3)、方案（2）若仅满足∠ABD＝∠BDE≠90°，BC＝CD，方案（2）（填“可行”或“不可行”）.

查看试题解析
26. 如图，在等边 $△ A B C$ 中， $A B = A C = B C = 10$ 厘米， $D C = 4$ 厘米，如果点M以3厘米/秒的速度运动从点C到点B运动.

(1)、经过多少秒后， $△ C D M$ 是等边三角形？

(2)、若点N在线段 $B A$ 上由B点向A点运动.点N和点M同时出发，若点N的运动速度与点M的运动速度相等.当两点的运动时间为多少时， $△ B M N$ 是一个直角三角形？

(3)、若点N的运动速度与点M的运动速度不相等，点N从点B出发，点M以原来的运动速度从点C同时出发，都是顺时针沿△ABC三边运动，经过20秒，点M与点N第一次相遇，则点N的运动速度是多少厘米/秒？

查看试题解析