广东省深圳市福田区2022-2023学年七年级上学期数学期中测试题

试卷更新日期：2022-11-28 类型：期中考试

进入出卷网下载

一、选择题（本题共10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的）

1. 2022的倒数是（）

A、-2022 B、2022 C、 $\frac{1}{2022}$ D、 $- \frac{1}{2022}$

查看试题解析
2. 下列各图中，可以是一个正方体的平面展开图的是（）

A、 B、 C、 D、

查看试题解析
3. 拒绝“餐桌浪费”，刻不容缓．据统计全国每年浪费食物总量约45000000000千克，这个数据用科学记数法表示为（）

A、4.5×10¹⁰千克 B、4.5×10⁹千克 C、45×10⁹千克 D、0.45×10¹¹千克

查看试题解析
4. 在 $- \frac{7}{10}$ ， 0，-|-5|，-0.6，2， $- (- \frac{1}{3})$ ， -10中负数的个数有（）

A、3 B、4 C、5 D、6

查看试题解析
5. 用一平面去截下列几何体，其截面不可能是长方形的是（）

A、 B、 C、 D、

查看试题解析
6. 下列代数式符合规范书写要求的是（）

A、-1x B、 $1 \frac{1}{5}$ xy C、0.3÷x D、 $- \frac{5}{2}$ a

查看试题解析
7. 在数轴上表示3的点与表示-4的点之间的距离是（）

A、-7 B、7 C、-2 D、4

查看试题解析
8. 有理数a、b在数轴上的位置如图所示，则下列各式错误的是（）

A、b<0<a B、|b|>|a| C、a+b<0 D、b-a>0

查看试题解析
9. 华为技术有限公司今年1月份产值a亿元，2月份比1月份减少了10%，则2月份产值达到（）

A、（1-10%） a亿元 B、10%亿元 C、（a-10%）亿元 D、 $\frac{a}{1 - 10 %}$ 亿元

查看试题解析
10. 下列说法：
①若一个数的倒数等于它本身，则这个数是1或-1；②|a|= |-2|，则a=-2；

③2³x²y+x+1是六次三项式；④若a，b互为相反数，则a+b=0．

其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共5小题，每小题3分，共15分）

11. 如果向东走3米记作＋3米，那么向西走5米记作米

查看试题解析
12. 在-2，0，1，-1这四个数中，最小的有理数是.

查看试题解析
13. 若|a+3|+（b-2）²=0，则a+b=.

查看试题解析
14. 如图是正方体的展开图，那么原正方体中，与“党”字所在面对面上的汉字是.

查看试题解析
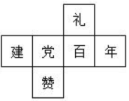15. 已知a为有理数，如果规定一种新的运算“※”，规定： a※b=3a-5b，例如：1※2=3×1-5×2=3-10=-7，计算：（4※2）※5=.

查看试题解析

三、解答题（本大题共7小题，其中第16题18分，第17题6分，第18题6分，第19题6分，第20题6分，第21题8分，第22题5分，共55分）

16. 计算：

(1)、7+（-8）-（-9）

(2)、（-2）×6-6÷3

(3)、（-3）÷ $\frac{3}{4}$ ×2×（-5）

(4)、（ $\frac{1}{4} - \frac{2}{3}$ ）×（-24）

(5)、（-3）³÷（-9）+（-2）²-×|-4+1|

(6)、-1⁴-（-10）÷ $\frac{1}{2}$ ×2

查看试题解析
17. 用数轴上的点表示下列各数： $\frac{3}{2}$ ，-2.5， $- \frac{1}{2}$ ，0， $\frac{4}{5}$ ，并用“ $<$ ”把它们连接起来．

查看试题解析
18.
如图是小强用七块相同的小立方体搭成的一个几何体，从正面、左面和上面观察这个几何体，请你在下面相应的位置分别画出你所看到的几何体的形状图．

查看试题解析
19. 一只蚂蚁从某点A出发，在一条直线上来回爬行，假定把向右爬行的路程记为正数，向左爬行的路程记为负数，则爬行各段路程（单位：厘米）依次为：+2，-3，+12，-8，-7，+16，-12，

(1)、通过计算说明蚂蚁是否回到起点A；

(2)、如果蚂蚁爬行的速度为0.5厘米/秒，那么蚂蚁共爬行了多长时间．

查看试题解析
20. 已知a，b互为倒数，c，d（d≠0）互为相反数，|m|=2．根据已知条件请回答：

(1)、ab= ， c+d= ， $\frac{c}{d}$ = ， m= ．

(2)、求： $\frac{m}{2} + a b + \frac{c + d}{3 m} - {(\frac{c}{d})}^{2012}$ 的值．

查看试题解析
21. 在数轴上点A表示数a，点B表示数b，点C表示数c，并且a是多项式-2x²-4x+1的一次项系数，b 是最小的正整数，单项式 $- \frac{1}{2}$ x²y⁴的次数为c．

(1)、a= ， b= ， c= ．

(2)、若将数轴在点B处折叠，则点A与点C 重合（填“能”或“不能”）；

(3)、若数轴上M、N两点之间的距离为2022（M在N的左侧），且M、N两点在B处折叠后互相重合，则M、N表示的数分别是：M：；N：

(4)、若在数轴上任意画出一条长是2022个单位的线段，则此线段盖住的整数点的个数是。

查看试题解析
22. 阅读材料：求1+2+2²+2³+……+2¹⁰⁰的值.
解：设S=1+2+2²+2³+……+2¹⁰⁰
将等式两边同时乘以2得
2S=2+2²+2³+2⁴……+2¹⁰¹
因此2S-S=（2+2²+2³+2⁴……+2¹⁰¹） - （1+2+2²+2³+……+2¹⁰⁰） =2¹⁰¹-1
所以S=2¹⁰¹-1
即1+2+2²+2³+……+2¹⁰⁰=2¹⁰¹-1
请你仿照此法计算：

(1)、1+2+2²+2³+2⁴+2⁵=

(2)、求1+3+3²+……+3¹⁰¹的值.

查看试题解析