2022-2023学年冀教版数学八年级上册期末模拟试卷3

试卷更新日期：2022-11-28 类型：期末考试

进入出卷网下载

一、单选题（每题3分，共36分）

1. 下列计算正确的是（）

A、 $(- \sqrt{16})^{2} = 16$ B、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ C、 $\sqrt[3]{- 1} = 1$ D、 $\sqrt[3]{9} = 3$

查看试题解析
2. 把分式 $\frac{3 a b}{a + b}$ 中的a，b都扩大到原来的2倍，则分式的值（）

A、扩大到原来的6倍 B、扩大到原来的4倍 C、扩大到原来的2倍 D、不变

查看试题解析
3. 下列二次根式能与 $\sqrt{3}$ 合并的是（）．

A、 $\sqrt{12}$ B、 $\sqrt{10}$ C、 $\sqrt{8}$ D、 $\sqrt{6}$

查看试题解析
4. 如图所示 $A B = A C$ ，要说明 $△ A E B$ ≌ $△ A D C$ ，需添加的条件不能是（）

A、 $∠ B = ∠ C$ B、 $A E = A D$ C、 $B E = C D$ D、 $∠ A E B = ∠ A D C$

查看试题解析
5. 如图，在△ABC中，∠C＝90°，使点P到AB、BC的距离相等，则符合要求的作图痕迹（　　）

A、 B、 C、 D、

查看试题解析
6. 等腰三角形底边长为5，一腰上的中线把周长分成两部分的差为3，则腰长为（）

A、2 B、8 C、2或8 D、10

查看试题解析
7. 老师设计了接力游戏，用合作的方式完成分式化简规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简过程如图所示：
老师 $\frac{x^{2} - 2 x}{x - 1} \div \frac{x^{2}}{1 - x}$ →甲 $\frac{x^{2} - 2 x}{x - 1} \cdot \frac{1 - x}{x^{2}}$ →乙 $\frac{x^{2} - 2 x}{x - 1} \cdot \frac{x - 1}{x^{2}}$ →丙 $\frac{x (x - 2)}{x - 1} \cdot \frac{x - 1}{x^{2}}$ →丁 $\frac{x - 2}{2}$
接力中，自己负责的一步出现错误的是（）

A、只有乙 B、甲和丁 C、乙和丙 D、乙和丁

查看试题解析
8. 已知实数 $a$ 在数轴上的对应点位置如图所示，则化简 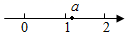$| a - 1 | - \sqrt{{(a - 2)}^{2}}$ 的结果是（）

A、 $3 - 2 a$ B、 $- 1$ C、1 D、 $2 a - 3$

查看试题解析
9. 如图，OP平分∠MON，PE⊥OM于点E，PF⊥ON于点F，OA＝OB，则图中有（）对全等三角形．

A、2 B、3 C、4 D、5

查看试题解析
10. 点P在 $∠ A O B$ 的角平分线上，点P到 $O A$ 边的距离为10，点Q是 $O B$ 边上任意一点，则 $P Q$ 的最小值为（）

A、6 B、8 C、10 D、12

查看试题解析
11. 随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，公司投递快件的能力由每周3000件提高到4200件，平均每人每周比原来多投递40件，若快递公司的快递员人数不变，求原来平均每人每周投递快件多少件？设原来平均每人每周投递快件x件，根据题意可列方程为（）

A、 $\frac{3000}{x}$ ＝ $\frac{4200}{x - 40}$ B、 $\frac{3000}{x} + 40 = \frac{4200}{x}$ C、 $\frac{4200}{x}$ ＝ $\frac{3000}{x}$ ﹣40 D、 $\frac{3000}{x}$ ＝ $\frac{4200}{x + 40}$

查看试题解析
12. 如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连结CE交AD于点F，连结BD交CE于点G，连结BE.下列结论：①CE＝BD；②△ADC是等腰直角三角形；③∠ADB＝∠AEB；④S_四边形_BCDE＝ $\frac{1}{2}$ BD·CE；⑤BC²＋DE²＝BE²＋CD².其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每空3分，共18分）

13. $\sqrt{16}$ 的平方根是， $2 - \sqrt{5}$ 的绝对值是.

查看试题解析
14. 若分式方程 $\frac{1}{x - 3} - 1 = \frac{a x}{x - 3}$ 的无解，则 $a$ ＝．

查看试题解析
15. 如图， $A D$ 是 $△ A B C$ 的角平分线， $∠ C = 90^{\circ} ， C D = 3 cm$ ，点P是 $A B$ 上一动点，连接 $D P$ ，则 $D P$ 的最小值为cm，.

查看试题解析
16. 若 $\frac{1}{\sqrt{1 - 2 x}}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
17. 某中学假期后勤中的一项工作是请 $30$ 名木工制作200把椅子和100张课桌，已知一名工人在单位时间内可以制作10把椅子或7张课桌，将这30名工人分成两组，一组制作课桌，一组制作椅子，两组同时开工．应分配人制作课桌，才能使完成此项工作的时间最短．

查看试题解析
18. 如图，△ABC中，∠ACB=90°，AC∥BD，BC=BD，在AB上截取BE，使BE=BD，过点B作AB的垂线，交CD于点F，连接DE，交BC于点H，交BF于点G，BC=7，BG=4，则AB=.

查看试题解析

三、解答题（共6题，共46分）

19.

(1)、先化简，再求值： $\frac{x^{2} - 4}{x^{2} - 9} \div (1 - \frac{1}{x + 3})$ ，其中 $x = 2^{0} + {(\frac{1}{3})}^{- 1}$ ．

(2)、解分式方程： $\frac{x}{x + 2} = \frac{x + 1}{x - 1}$

查看试题解析
20. 如图，在△ABC中，边BC，AB上的高AD，CE相交于点F，且∠ACE＝45°，连接BF，求∠BFE的度数．

查看试题解析
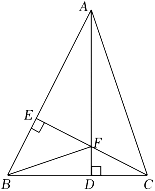21. 作图题：要求保留作图痕迹，不写作法

(1)、作线段AC的垂直平分线，分别交AC、BC于E、F.在直线EF上找一点P，使得点P到射线AB，AC的距离相等.

(2)、若AB＝6，BC＝8，连接AF，求△ABF的周长.

查看试题解析
22. 我们之前学习有理数时，知道两个数的乘积为1则这两个数互为倒数.在学习二次根式的过程中，小明研究发现有一些特殊的无理数之间具有互为倒数的关系.例如：由 $(\sqrt{2} + 1) (\sqrt{2} - 1) = 1$ ，可得 $\sqrt{2} + 1$ 与 $\sqrt{2} - 1$ 互为倒数，即 $\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ 或 $\frac{1}{\sqrt{2} - 1} = \sqrt{2} + 1$ ，类似地， $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2}) = 1$ ，可得 $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ 或 $\frac{1}{\sqrt{3} - \sqrt{2}} = \sqrt{3} + \sqrt{2}$
根据小明发现的规律，解决下列问题：

(1)、 $\frac{1}{\sqrt{7} + \sqrt{6}} =$ ， $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ $(n$ 为正整数）

(2)、若 $\frac{1}{2 \sqrt{3} + a} = 2 \sqrt{3} - a$ ，则 $a =$

(3)、求 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{100} + \sqrt{99}}$ 的值.

查看试题解析
23. 针对资源急需问题，某医疗设备公司紧急复工，但受疫情影响，医用防护服生产车间仍有7人不能到厂生产．为了应对疫情，已复产的工人加班生产，由原来每天工作8小时增加到10小时，每小时完成的工作量不变．原来每天能生产防护服800套，现在每天能生产防护服650套．

(1)、求原来生产防护服的工人有多少人？

(2)、复工10天后，未到的工人同时到岗加入生产，每天生产时间仍然为10小时．公司决定将复工后生产的防护服14500套捐献给某地，则至少还需要生产多少天才能完成任务？

查看试题解析
24. 思维启迪：

(1)、如图1，点P是线段 $A B$ ， $C D$ 的中点，则 $A C$ 与 $B D$ 的数量关系为，位置关系为；

(2)、思维探索：
①如图2，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，点D为 $△ A B C$ 内一点，连接 $B D$ ， $D C$ ，延长 $D C$ 到点E ，使 $C E = C D$ ，连接 $A E$ ，若 $B D ⊥ A E$ ，请用等式表示 $A B$ ， $B D$ ， $A E$ 之间的数量关系，并说明理由；
②如图3，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点D为 $A B$ 中点，点E在线段 $B D$ 上（点E不与点B ，点D重合），连接 $C E$ ，过点A作 $A F ⊥ C E$ ，连接 $F D$ .若 $A F = 8$ ， $C F =3$ ，请直接写出 $F D$ 的长.

查看试题解析