2022-2023学年冀教版数学八年级上册期末模拟试卷2
试卷更新日期:2022-11-27 类型:期末考试
一、单选题每题3分,共36分)
-
1. 下列说法正确的是( )A、-2是 的算术平方根 B、3是-9的算术平方根 C、16的平方根是±4 D、27的立方根是±32. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 无论a取何值,下列分式总有意义的是( )A、 B、 C、 D、4. 下列各式正确的是( )A、 B、 C、 D、5. 下列命题中,是真命题的是( )A、全等三角形的对应角相等 B、面积相等的两个三角形是全等三角形 C、的解是 D、如果 , 则6. 如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( )
3. 无论a取何值,下列分式总有意义的是( )A、 B、 C、 D、4. 下列各式正确的是( )A、 B、 C、 D、5. 下列命题中,是真命题的是( )A、全等三角形的对应角相等 B、面积相等的两个三角形是全等三角形 C、的解是 D、如果 , 则6. 如图,DE是△ABC的边BC的垂直平分线,分别交边AB,BC于点D,E,且AB=9,AC=6,则△ACD的周长是( ) A、10.5 B、15 C、12 D、187. 已知关于x的分式方程的解是正数,则m的取值范围是( )A、 B、 C、且 D、且8. 已知的两条高线交于点 , 若 , 则的度数为( )A、 B、 C、或 D、或9. 新型冠状病毒颗粒近似呈球状,其直径介于 , 平均为 , 若 , 则可以用科学记数法表示为( )A、 B、 C、 D、10. 如图,在中, , 直角的顶点P是的中点,两边、分别交、于点E、F.当在内绕点P旋转时,对于下列结论:①;② , ③;④ , 其中正确结论有( )
A、10.5 B、15 C、12 D、187. 已知关于x的分式方程的解是正数,则m的取值范围是( )A、 B、 C、且 D、且8. 已知的两条高线交于点 , 若 , 则的度数为( )A、 B、 C、或 D、或9. 新型冠状病毒颗粒近似呈球状,其直径介于 , 平均为 , 若 , 则可以用科学记数法表示为( )A、 B、 C、 D、10. 如图,在中, , 直角的顶点P是的中点,两边、分别交、于点E、F.当在内绕点P旋转时,对于下列结论:①;② , ③;④ , 其中正确结论有( ) A、1个 B、2个 C、3个 D、4个11. 已知实数a满足条件 ,那么 的值为A、2010 B、2011 C、2012 D、201312. 如图,已知在正方形中,厘米, , 点E在边上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向D点运动,设运动时间为t秒,当ΔBPE与ΔCQP全等时,t的值为( )
A、1个 B、2个 C、3个 D、4个11. 已知实数a满足条件 ,那么 的值为A、2010 B、2011 C、2012 D、201312. 如图,已知在正方形中,厘米, , 点E在边上,且厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向D点运动,设运动时间为t秒,当ΔBPE与ΔCQP全等时,t的值为( )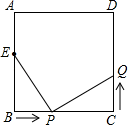 A、2 B、2或1.5 C、2.5 D、2.5或2
A、2 B、2或1.5 C、2.5 D、2.5或2二、填空题(每空3分,共18分)
-
13. 若最简二次根式 与 是同类根式,则 .14. “绿水青山就是金山银山”.某地为美化环境,计划种植树木2000棵.由于志愿者的加入,实际每天植树的棵树比原计划增加了25%,结果提前4天完成任务.则实际每天植树棵.15. 如图,分别作出点P关于OA、OB的对称点P1、P2 , 连接P1P2 , 分别交OA、OB于点M、N,若P1P2=5cm,则△PMN的周长为 .
 16. 的算术平方根是 , ﹣2绝对值是 , 的倒数是 .17. 如图,以直角三角形的三边为边向外作三个正方形A、B、C . 若 , ,则 .
16. 的算术平方根是 , ﹣2绝对值是 , 的倒数是 .17. 如图,以直角三角形的三边为边向外作三个正方形A、B、C . 若 , ,则 . 18. 已知 ,则式子 的值等于
18. 已知 ,则式子 的值等于三、解答题(共7题,共66分)
-
19. 计算: .20. 先化简 ,再从0,1,2中选取一个合适的x的值代入求值.21. 如图,在中,
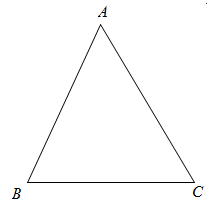
( 1 )尺规作图:作的平分线;
( 2 )尺规作图:作线段的垂直平分线;(不写作法,保留作图痕迹)
( 3 )若与交于点 , ∠ACP=24°,求的度数.
22. 小明在解决问题:已知 ,求 的值,他是这样分析与解答的:,
,
,
.
.
请你根据小明的分析过程,解决如下问题:若 ,求 的值.
23. 如图,在中, , 点D是线段上一点,以为腰作等腰直角 , 使 , 于点G,交于点F.求证: . 24. 某地为某校师生交通方便,在通往该学校原道路的一段全长为300 m的旧路上进行整修铺设柏油路面.铺设120 m后,为了尽量减少施工对城市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用30天完成这一任务.(1)、求原计划每天铺设路面的长度;(2)、若市政部门原来每天支付工人工资为600元,提高工效后每天支付给工人的工资增长了30%,现市政部门为完成整个工程准备了25 000元的流动资金.请问,所准备的流动资金是否够支付工人工资?并说明理由.25. 如图,在等腰中, , , 是的高,是的角平分线,与交于点当的大小变化时,的形状也随之改变.
24. 某地为某校师生交通方便,在通往该学校原道路的一段全长为300 m的旧路上进行整修铺设柏油路面.铺设120 m后,为了尽量减少施工对城市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用30天完成这一任务.(1)、求原计划每天铺设路面的长度;(2)、若市政部门原来每天支付工人工资为600元,提高工效后每天支付给工人的工资增长了30%,现市政部门为完成整个工程准备了25 000元的流动资金.请问,所准备的流动资金是否够支付工人工资?并说明理由.25. 如图,在等腰中, , , 是的高,是的角平分线,与交于点当的大小变化时,的形状也随之改变. (1)、当时,求的度数;(2)、设 , , 求变量与的关系式;(3)、当是等腰三角形时,求的度数.
(1)、当时,求的度数;(2)、设 , , 求变量与的关系式;(3)、当是等腰三角形时,求的度数.